
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球中没有红球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望。
的分布列和数学期望。
(1)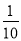 ;(2)
;(2)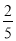 ;(3)
;(3)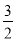 ;
;
【解析】
试题分析:(1)取出的4个球没有红球即均为黑色球包括从甲盒内取出的2个球均黑球且从乙盒内取出的2个球为黑球,这两个事件是相互独立的,根据相互独立事件同时发生的概率得到结果.
(2)取出的4个球中恰有1个红球有:?从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球;?从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球两种情况,它们是互斥的.
(3)ξ为取出的4个球中红球的个数,则ξ可能的取值为0,1,2,3.结合前两问的解法得到结果,由此得出分布列和期望.
试题解析:【解析】
(1)设“取出的4个球中没有红球”为事件A。
则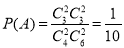 ,
,
所以取出的4个球中没有红球的概率为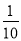 。 4分
。 4分
(2)【解析】
设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件B,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件C。由于事件B,C互斥,
且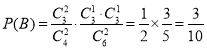 , 6分
, 6分
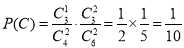 。 8分
。 8分
所以,取出的4个球中恰有1个红球的概率为
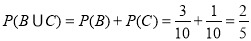 。 9分
。 9分
(3)【解析】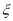 可能的取值为0,1,2,3。 10分
可能的取值为0,1,2,3。 10分
由(1)(2)知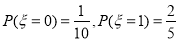 。
。
 。
。
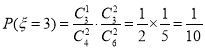 ,
,
所以,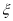 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
12分
所以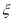 的数字期望
的数字期望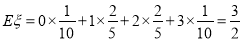 。 13分
。 13分
考点:1、互斥事件;2、相互独立事件;3离散型随机变量的分布列及期望;


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年河南省富洲部高二上学期9月考试数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”
B.命题“?x0∈R,x02+x0-1<0”的否定是“?x∈R,x2+x-1>0”
C.命题“若x=y,则sin x=sin y”的逆否命题为假命题
D.若“p或q”为真命题,则p,q中至少有一个为真命题
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省西区高一9月月考数学试卷(解析版) 题型:解答题
(本小题12分)
我国是水资源匮乏的国家为鼓励节约用水,某市打算出台一项水费政策措施,规定:每一季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%,如果某人本季度实际用水量为 吨,
吨,
应交水费为 .
.
(1)求 、
、 、
、 的值;
的值;
(2)试求出函数 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二下学期期末考试理科数学试卷(解析版) 题型:填空题
抛掷一个骰子,若掷出5点或6点就说试验成功,则在3次试验中恰有2次成功的概率为__________。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)各项均不相等的等差数列 的前四项的和为
的前四项的和为 ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式 与前n项和
与前n项和 ;
;
(2)记 为数列
为数列 的前n项和,求
的前n项和,求
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com