
设z=2x+y,式中变量满足下列条件: 求z的最大值和最小值.
求z的最大值和最小值.
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第四章第2课时练习卷(解析版) 题型:填空题
在平行四边形ABCD中,AC为一条对角线,若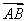 =(2,4),
=(2,4),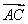 =(1,3),则
=(1,3),则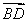 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:解答题
某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:填空题
若直线y=2x上存在点(x,y)满足约束条件 则实数m的最大值为________.
则实数m的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:填空题
已知实数x、y满足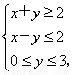 则z=2x+y的最小值是________.
则z=2x+y的最小值是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:解答题
甲厂以x千克/小时的速度运输生产某种产品(生产条件要求1≤x≤10),每小时可获得利润是100(5x+1- )元.
)元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如图,在三棱柱ABCA1B1C1中,A1B⊥平面ABC,AB⊥AC,且AB=AC=A1B=2.
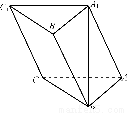
(1)求棱AA1与BC所成的角的大小;
(2)在棱B1C1上确定一点P,使二面角P-AB-A1的平面角的余弦值为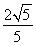 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
如图,在正三棱柱ABCDEF中,AB=2,AD=1.P是CF的延长线上一点,FP=t.过A、B、P三点的平面交FD于M,交FE于N.
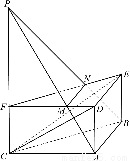
(1)求证:MN∥平面CDE;
(2)当平面PAB⊥平面CDE时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com