
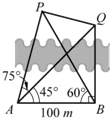
 (2013•辽宁二模)风景秀美的凤凰湖畔有四棵高大的银杏树,记做A、B、P、Q,欲测量P、Q两棵树和A、P两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得A、B两点间的距离为AB=100米,如图,同时也能测量出∠PAB=75°,∠QAB=45°,∠PBA=60°,∠QBA=90°,则P、Q两棵树和A、P两棵树之间的距离各为多少?
(2013•辽宁二模)风景秀美的凤凰湖畔有四棵高大的银杏树,记做A、B、P、Q,欲测量P、Q两棵树和A、P两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得A、B两点间的距离为AB=100米,如图,同时也能测量出∠PAB=75°,∠QAB=45°,∠PBA=60°,∠QBA=90°,则P、Q两棵树和A、P两棵树之间的距离各为多少?| AP |
| sin60° |
| 100 |
| sin45° |
| 6 |
| 2 |
| 6 |
| 2 |
| 6 |
| 2 |
| 2 |
| 2 |
| 6 |


科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com