
分析 由题意,本题属于几何概型的概率求法,由此只要求出所有事件的区域长度以及满足条件的m的范围对应的区域长度,利用几何概型概率公式可求.
解答 解:∵f(x)=$\frac{1}{3}$x3-x2+mx,
∴f′(x)=x2-2x+m,∴导函数为抛物线,开口向上,
∵要使f(x)在R上单调,
∴f'(x)=x2-2x+m≥0在R上恒成立,即m≥-x2+2x在R上恒成立,
∴m大于等于-x2+2x的最大值即可,
∵-x2+2x=-(x-1)2+1≤1,
∴m≥1,
∵m≤4,∴1≤m≤4,长度为3,
∵区间[0,4]上任意取一个数m,长度为4,
∴函数f(x)=$\frac{1}{3}$x3-x2+mx是R上的单调函数的概率是$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题主要考查几何概型,考查利用导数研究函数的单调性,正确把握导数的正负与函数单调性之间的关系是关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{37}{16}$ | B. | $\frac{11}{5}$ | C. | $\sqrt{10}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
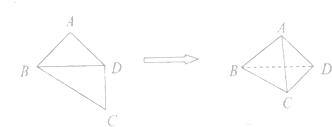
| A. | $\frac{8\sqrt{2}}{3}$π | B. | 24π | C. | 4$\sqrt{3}$π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (一∞,1) | B. | (2,+∞) | C. | (1,2) | D. | (一∞,1)U(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com