
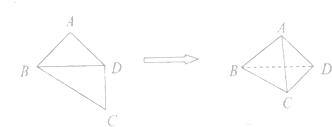
| A. | $\frac{8\sqrt{2}}{3}$π | B. | 24π | C. | 4$\sqrt{3}$π | D. | 12π |
分析 由题意可知,四面体A'-BCD顶点在同一个球面上,BC的中点就是球心,求出球的半径,即可得到球的体积.
解答 解:平面四边形ABCD中,AB=AD=CD=2,BD=2$\sqrt{2}$,BD⊥CD,将其沿对角线BD折成四面体A'-BCD,
使平面A'BD⊥平面BCD.四面体A'-BCD顶点在同一个球面上,△BCD和△A'BC都是直角三角形,
BC的中点就是球心,所以BC=2$\sqrt{3}$,球的半径为:$\sqrt{3}$;
所以球的体积为:$\frac{4π}{3}×(\sqrt{3})^{3}$=4$\sqrt{3}π$.
故选:C.
点评 本题是基础题,考查四面体的外接球的体积的求法,找出外接球的球心,是解题的关键,考查计算能力,空间想象能力.


科目:高中数学 来源: 题型:选择题
| A. | 命题:“若y=f(x)是幂函数,则y=f(x)的图象不经过第四象限”的否命题是假命题 | |
| B. | 设a,b∈R,则“a>b”是“a|a|>b|b|”的充要条件 | |
| C. | 命题“?n∈N*,f(n)∈N*且f(n)≤n”的否定形式是“?n0∈N*,f(n0)∉N*且f(n0)≥n0” | |
| D. | 若p∨q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
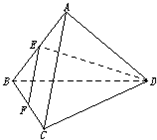 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校教务处对本校高三文科学生第一次模拟考试的数学成绩进行分析,用分层抽样方法抽取了20名学生的成绩,分数用茎叶图记录如图所示(部分数据丢失),并绘制如下频率分布表:
某校教务处对本校高三文科学生第一次模拟考试的数学成绩进行分析,用分层抽样方法抽取了20名学生的成绩,分数用茎叶图记录如图所示(部分数据丢失),并绘制如下频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] | 合计 |
| 频数 | b | |||||
| 频率 | a | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com