
分析 利用角的范围求出相位的范围,通过正弦函数的有界性求解即可.
解答 解:$x∈[{-\frac{2}{3},\frac{5}{3}}]$,可得$\frac{πx}{2}+\frac{π}{6}$∈[$-\frac{π}{6}$,π],
$f(x)=sin(\frac{πx}{2}+\frac{π}{6})+1$∈[$1-\frac{\sqrt{3}}{2}$,2].当$\frac{πx}{2}+\frac{π}{6}$=$-\frac{π}{6}$时,函数取得最小值;
当$\frac{πx}{2}+\frac{π}{6}$=$\frac{π}{2}$时,函数取得最大值;
故答案为:[$\frac{1}{2}$,2].
点评 本题考查三角函数的有界性,函数的值域的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{3}{2}$ | C. | -$\frac{3}{2}$或0 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{{e}^{2}+1}{e}$) | B. | ($\frac{{e}^{2}+1}{e}$,+∞) | C. | $(-\frac{{{e^2}+1}}{e},-2)$ | D. | $(2,\frac{{{e^2}+1}}{e})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.
如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{37}{16}$ | B. | $\frac{11}{5}$ | C. | $\sqrt{10}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
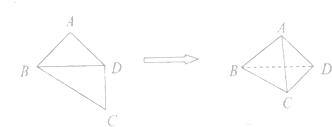
| A. | $\frac{8\sqrt{2}}{3}$π | B. | 24π | C. | 4$\sqrt{3}$π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
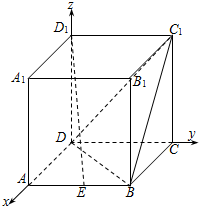 已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com