
 如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.
如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.分析 (1)分别求出甲、乙训练的成绩的平均数和方差,由此能求出结果.
(2)当乙选取5环时,一定满足要求,当乙选取7环时,甲只能从9环、10环中选取,从而求出甲的成绩大于乙的成绩的概率,ξ的取值分别是0,1,2,3,4,且ξ~B(4,$\frac{3}{8}$),由此能求出ξ的分布列和数学期望.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{4}$(6+7+9+10)=8,
$\overline{{x}_{乙}}$=$\frac{1}{4}$(5+7+10+10)=8,
${{S}_{甲}}^{2}$=$\frac{1}{4}$[(6-8)2+(7-8)2+(9-8)2+(10-8)2]=$\frac{5}{2}$,
${{S}_{乙}}^{2}$=$\frac{1}{4}$[(5-8)2+(7-8)2+(10-8)2+(10-8)2]=$\frac{9}{2}$,
∵$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${{S}_{甲}}^{2}$<${{S}_{乙}}^{2}$,
∴甲运动员的射击水平平稳.
(2)当乙选取5环时,一定满足要求,此时的概率为p1=$\frac{1}{4}×1=\frac{1}{4}$,
当乙选取7环时,甲只能从9环、10环中选取,此时的概率为${p}_{2}=\frac{1}{4}×\frac{1}{2}=\frac{1}{8}$,
∴甲的成绩大于乙的成绩的概率为p=p1+p2=$\frac{1}{4}+\frac{1}{8}=\frac{3}{8}$.
依题意,ξ的取值分别是0,1,2,3,4,且ξ~B(4,$\frac{3}{8}$),
∴p(ξ=0)=${({\frac{5}{8}})^4}=\frac{625}{4096}$,
p(ξ=1)=$C_4^1\frac{3}{8}{({\frac{5}{8}})^3}=\frac{375}{1024}$,
$p({ξ=2})=C_4^2{({\frac{3}{8}})^2}{({\frac{5}{8}})^2}=\frac{675}{2048}$,
$p({ξ=3})=C_4^3{({\frac{3}{8}})^3}\frac{5}{8}=\frac{135}{1024}$,
$p({ξ=4})={({\frac{3}{8}})^4}=\frac{81}{4096}$,
因此,ξ的分布列如下:
| ζ | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{625}{4096}$ | $\frac{375}{1024}$ | $\frac{675}{2048}$ | $\frac{135}{1024}$ | $\frac{81}{4096}$ |
点评 本题考查平均数、方差的求法及应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -2-5i | B. | -2+5i | C. | 2+5i | D. | 2-5i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{6},0})$ | B. | $({\sqrt{2},0})$ | C. | (6,0) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
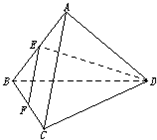 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,lnx+$\frac{1}{lnx}$≥2 | B. | 当x>0时,$\sqrt{x}$+$\frac{1}{\sqrt{x}}$≥2 | ||
| C. | 当x≥2时,x+$\frac{1}{x}$的最小值为2 | D. | 当0<x≤π时,sinx+$\frac{4}{sinx}$最小值为4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com