
| A. | 当x>0且x≠1时,lnx+$\frac{1}{lnx}$≥2 | B. | 当x>0时,$\sqrt{x}$+$\frac{1}{\sqrt{x}}$≥2 | ||
| C. | 当x≥2时,x+$\frac{1}{x}$的最小值为2 | D. | 当0<x≤π时,sinx+$\frac{4}{sinx}$最小值为4 |
分析 逐个判断各个选项的正误,在解答过程中注意等号成立的条件和符号.
解答 解:
A、取x=$\frac{1}{e}$,得到$lnx+\frac{1}{lnx}=-2<0$,故A错误;
B、当x>0时,$\sqrt{x}+\frac{1}{\sqrt{x}}≥2\sqrt{\sqrt{x}•\frac{1}{\sqrt{x}}}=2$,故B正确;
C、显然当x≥2时,$x+\frac{1}{x}≥2+\frac{1}{x}>2$,故C错误;
D、$sinx+\frac{4}{sinx}≥2\sqrt{sinx•\frac{4}{sinx}}=4$,“=“当且仅当“$sinx=\frac{4}{sinx}$即sinx=2”时成立,显然错误.
综上所述,答案选B.
点评 本题考查基本不等式的应用.使用基本不等式的前提条件的判断是本题的易错点.


科目:高中数学 来源: 题型:解答题
 如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.
如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
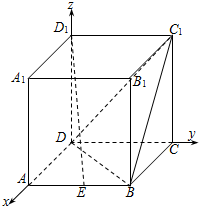 已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com