
分析 (1)根据同底数幂相乘,底数不变,指数相加,可计算结果;
(2)将原式化为:$[(\frac{3}{2})^{3}]^{-\frac{2}{3}}$-$\sqrt{\frac{49}{9}}$+${[{(\frac{1}{5})}^{3}]}^{-\frac{2}{3}}$×$\frac{2}{25}$,进而可得计算结果.
解答 解:(1):(-2x${\;}^{\frac{1}{4}}$y${\;}^{-\frac{1}{3}}$)(3x${\;}^{-\frac{1}{2}}$y${\;}^{\frac{2}{3}}$)(-4x${\;}^{\frac{1}{4}}$y${\;}^{\frac{2}{3}}$)
=(-2)×3×(-4)${x}^{\frac{1}{4}-\frac{1}{2}+\frac{1}{4}}$${y}^{-\frac{1}{3}+\frac{2}{3}+\frac{2}{3}}$
=24y;
(2):($\frac{27}{8}$)${\;}^{-\frac{2}{3}}$-($\frac{49}{9}$)0.5+(0.008)${\;}^{-\frac{2}{3}}$×$\frac{2}{25}$.
=$[(\frac{3}{2})^{3}]^{-\frac{2}{3}}$-$\sqrt{\frac{49}{9}}$+${[{(\frac{1}{5})}^{3}]}^{-\frac{2}{3}}$×$\frac{2}{25}$.
=$\frac{4}{9}$-$\frac{7}{3}$+2
=$\frac{1}{9}$
点评 本题考查的知识点是有理数指数幂的化简求值,难度不大,属于基础是.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,lnx+$\frac{1}{lnx}$≥2 | B. | 当x>0时,$\sqrt{x}$+$\frac{1}{\sqrt{x}}$≥2 | ||
| C. | 当x≥2时,x+$\frac{1}{x}$的最小值为2 | D. | 当0<x≤π时,sinx+$\frac{4}{sinx}$最小值为4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2036 | B. | 4072 | C. | 4076 | D. | 2026 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
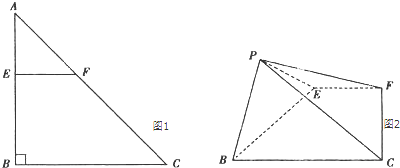
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
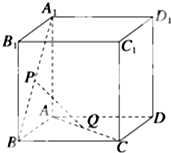 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com