
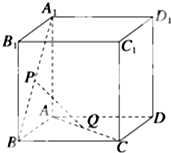
 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.分析 ①由题意:P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.则P,Q分别是A1B,AC的中点.取A1 A,AD的中点N,F,连接PN,NF,QF,可得面面平行转化成线面平行.
②通过补形在该正方体右边补一个正方体CC1D1D-C2C3 D3D2,C2 D2 的中点为M1,PQ∥FN∥A1D,那么角A1 D M1为异面直线PQ与AM的夹角.
解答 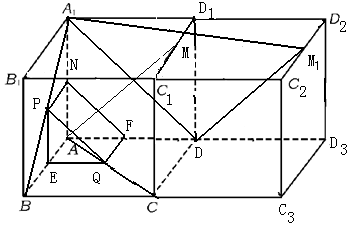 解:①证明:由题意:P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.则P,Q分别是A1B,AC的中点.取A1 A,AD的中点N,F,连接PN,NF,QF,可得PQ∥FN,NF∥平面BCC1B1.
解:①证明:由题意:P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.则P,Q分别是A1B,AC的中点.取A1 A,AD的中点N,F,连接PN,NF,QF,可得PQ∥FN,NF∥平面BCC1B1.
∴PQ∥平面BCC1B1.
②在该正方体右边补一个正方体C C2 D2D-C1 C3 D3 D1,C3 D3 的中点为M1,PQ∥FN∥A1D,那么∠A1 D M1为异面直线PQ与AM的夹角.
∵$\begin{array}{l}{A_1}D=\sqrt{2},D{M_1}=\sqrt{1+\frac{5}{4}}=\frac{3}{2},{A_1}{M_1}=\sqrt{{2^2}+\frac{1}{4}}=\frac{{\sqrt{17}}}{2}\\∴{A_1}{D^2}+D{M_1}^2={A_1}{M_1}^2\end{array}$
所以在三角形A1 D M1中,角A1 D M1为90°,即为PQ与Ma所成角的值为90°.
点评 本题考查了直线与平面平行的证明和异面直线所成的角的求法.补形法也是一直常见的方法.属于中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x∈Z|x<2} | B. | {x∈Z|0≤x<2} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com