
分析 方法一:分别画出y=ax与y=ex的图形,结合图可知答案,
方法二:命题“?x0∈[0,2],f(x0)>g(x0)的否定是“?x∈[0,2],ax≤ex”,然后同一可得.
解答 解法一:命题“?x0∈[0,2],f(x0)>g(x0)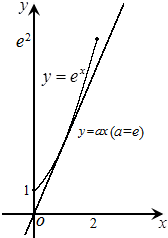
也就是命题“?x0∈[0,2],$a{x_0}>{e^{x_0}}$”,
若y=ax是y=ex的是y=ex的切线,
有a=e,切点横坐标x=1∈[0,2],
由图可知,只要a>e即可.
解法二:命题“?x0∈[0,2],f(x0)>g(x0)
的否定是“?x∈[0,2],ax≤ex”,
若y=ax是y=ex的是y=ex的切线,有a=e,切点横坐标x=1∈[0,2],
由图可知,a≤e时,命题“?x∈[0,2],ax≤ex”为真,
因此命题“?x0∈[0,2],$a{x_0}>{e^{x_0}}$”为真时,应该有a>e.
故答案为:(e,+∞)
点评 本题考查了函数存在性问题,以及参数的取值范围,属于中档题.


科目:高中数学 来源: 题型:解答题
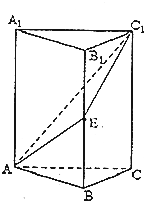 正三棱柱ABC-A1B1C1中,E为BB1的中点,AA1=2AB.
正三棱柱ABC-A1B1C1中,E为BB1的中点,AA1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
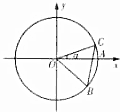 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为$(\frac{4}{5},-\frac{3}{5})$,∠AOC=α,若|BC|=1,则$\sqrt{3}{cos^2}\frac{α}{2}-sin\frac{α}{2}cos\frac{α}{2}-\frac{{\sqrt{3}}}{2}$的值为$\frac{3}{5}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为$(\frac{4}{5},-\frac{3}{5})$,∠AOC=α,若|BC|=1,则$\sqrt{3}{cos^2}\frac{α}{2}-sin\frac{α}{2}cos\frac{α}{2}-\frac{{\sqrt{3}}}{2}$的值为$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{{e}^{2}+1}{e}$) | B. | ($\frac{{e}^{2}+1}{e}$,+∞) | C. | $(-\frac{{{e^2}+1}}{e},-2)$ | D. | $(2,\frac{{{e^2}+1}}{e})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.
如图茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com