
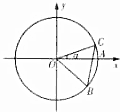
 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为$(\frac{4}{5},-\frac{3}{5})$,∠AOC=α,若|BC|=1,则$\sqrt{3}{cos^2}\frac{α}{2}-sin\frac{α}{2}cos\frac{α}{2}-\frac{{\sqrt{3}}}{2}$的值为$\frac{3}{5}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为$(\frac{4}{5},-\frac{3}{5})$,∠AOC=α,若|BC|=1,则$\sqrt{3}{cos^2}\frac{α}{2}-sin\frac{α}{2}cos\frac{α}{2}-\frac{{\sqrt{3}}}{2}$的值为$\frac{3}{5}$. 分析 根据三角函数的定义,结合三角函数的辅助角公式进行化简即可得到结论.
解答 解:∵点B的坐标为$(\frac{4}{5},-\frac{3}{5})$,设∠A0B=θ
∴sin(2π-θ)=$\frac{3}{5}$,cos(2π-θ)=$\frac{4}{5}$,
即sinθ=$\frac{3}{5}$,cosθ=$\frac{4}{5}$,
∵∠AOC=α,若|BC|=1,∴θ+α=$\frac{π}{3}$,
则α=$\frac{π}{3}$-θ,
则$\sqrt{3}{cos^2}\frac{α}{2}-sin\frac{α}{2}cos\frac{α}{2}-\frac{{\sqrt{3}}}{2}$=$\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα=cos(α+$\frac{π}{6}$)=cos($\frac{π}{2}$-θ)=sinθ=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题主要考查三角函数的化简和求值,利用三角函数的定义以及三角函数的辅助角公式是解决本题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
 如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,|AB|=$\sqrt{5}$,直线AB的斜率为-$\frac{1}{2}$,M是椭圆C长轴上的一个动点,设点M(m,0).
如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,|AB|=$\sqrt{5}$,直线AB的斜率为-$\frac{1}{2}$,M是椭圆C长轴上的一个动点,设点M(m,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{e}]$ | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | (-∞,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:“若y=f(x)是幂函数,则y=f(x)的图象不经过第四象限”的否命题是假命题 | |
| B. | 设a,b∈R,则“a>b”是“a|a|>b|b|”的充要条件 | |
| C. | 命题“?n∈N*,f(n)∈N*且f(n)≤n”的否定形式是“?n0∈N*,f(n0)∉N*且f(n0)≥n0” | |
| D. | 若p∨q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2-5i | B. | -2+5i | C. | 2+5i | D. | 2-5i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
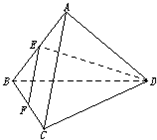 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com