
 ��ͼ��A��B����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����������㣬|AB|=$\sqrt{5}$��ֱ��AB��б��Ϊ-$\frac{1}{2}$��M����ԲC�����ϵ�һ�����㣬���M��m��0����
��ͼ��A��B����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����������㣬|AB|=$\sqrt{5}$��ֱ��AB��б��Ϊ-$\frac{1}{2}$��M����ԲC�����ϵ�һ�����㣬���M��m��0�������� ��������|AB|=$\sqrt{5}$��ֱ��AB��б��Ϊ-$\frac{1}{2}$�����������飬��������Բ�ķ��̣�
�������ֱ�߷��̣�������Բ���̣�����Τ�ﶨ���������ε������ʽ������֤�ý��ۣ�
�����ɣ���ֱ�����������ľ��빫ʽ��ϸ���ϵ���Ĺ�ϵ֤����
��� ���⣺��A��B����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����������㣬��|AB|=$\sqrt{5}$��ֱ��AB��б��Ϊ-$\frac{1}{2}$��
��A��a��0����B��0��b������|AB|=$\sqrt{{a}^{2}+{b}^{2}}=\sqrt{5}$��
��k=$\frac{b-0}{0-a}=-\frac{b}{a}=-\frac{1}{2}$�����a=2��b=1��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
����֤����ֱ��l�ķ���Ϊx=-2y+m����y=-$\frac{1}{2}$x+$\frac{m}{2}$���������$\frac{{x}^{2}}{4}+{y}^{2}=1$����ȥy��
������2x2-2mx+m2-4=0��
��C��x1��y1����D��x2��y2����
��x1+x2=m��x1x2=$\frac{1}{2}$m2-2��
�ǡ�OCM�������S1����ODN�������S2��
������M��m��0����N��0��$\frac{m}{2}$����
��x1+x2=m����|2y1|=|2��-$\frac{1}{2}$x1+$\frac{m}{2}$��|=|-x1+m|=|x2|��
��S��OCM=$\frac{1}{2}$|m||y1|��S��ODN=$\frac{1}{2}$|$\frac{m}{2}$||x2|��
���OCM��������ڡ�ODN�������
����֤�����ɣ���֪��M��m��0����x1+x2=m��x1x2=$\frac{1}{2}$m2-2��
��|CM|2+|MD|2=$��{x}_{1}-m��^{2}+{{y}_{1}}^{2}+��{x}_{2}-m��^{2}+{{y}_{2}}^{2}$=${{x}_{1}}^{2}-2m{x}_{1}+{m}^{2}+��-\frac{1}{2}{x}_{1}+\frac{m}{2}��^{2}$+${{x}_{2}}^{2}-2m{x}_{2}+{m}^{2}+��-\frac{1}{2}{x}_{2}+\frac{m}{2}��^{2}$
=$\frac{5}{4}��{x}_{1}+{x}_{2}��^{2}-\frac{5}{2}{x}_{1}{x}_{2}-\frac{5}{2}m��{x}_{1}+{x}_{2}��+\frac{5}{2}{m}^{2}$=$\frac{5}{4}{m}^{2}-\frac{5}{2}��\frac{1}{2}{m}^{2}-2��-\frac{5}{2}{m}^{2}+\frac{5}{2}{m}^{2}$=5��
���� ���⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ������ѧ���ļ��������������е��⣮


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2��a��2 | B�� | -2��a��2 | C�� | 0��a��2 | D�� | -2��a��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
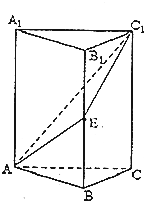 ��������ABC-A1B1C1�У�EΪBB1���е㣬AA1=2AB��
��������ABC-A1B1C1�У�EΪBB1���е㣬AA1=2AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 2015����CBA���й�����ְҵ�����������ܾ�����3��22�Ž����������ֶ�4��2սʤ����ҩ��������ɹ�����ͼ�DzμӴ˴��ܾ����ļס��������˶�Ա��
2015����CBA���й�����ְҵ�����������ܾ�����3��22�Ž����������ֶ�4��2սʤ����ҩ��������ɹ�����ͼ�DzμӴ˴��ܾ����ļס��������˶�Ա��| A�� | ${\overline{x}}_{��}$��${\overline{x}}_{��}$��$\overline{{S}_{��}}$��$\overline{{S}_{��}}$ | B�� | ${\overline{x}}_{��}$��${\overline{x}}_{��}$��$\overline{{S}_{��}}$��$\overline{{S}_{��}}$ | ||
| C�� | ${\overline{x}}_{��}$��${\overline{x}}_{��}$��$\overline{{S}_{��}}$��$\overline{{S}_{��}}$ | D�� | ${\overline{x}}_{��}$��${\overline{x}}_{��}$��$\overline{{S}_{��}}$��$\overline{{S}_{��}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
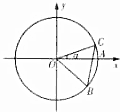 ��ͼ��ԲO��x���������Ľ���ΪA����C��B��ԲO�ϣ��ҵ�Cλ�ڵ�һ���ޣ���B������Ϊ$��\frac{4}{5}��-\frac{3}{5}��$����AOC=������|BC|=1����$\sqrt{3}{cos^2}\frac{��}{2}-sin\frac{��}{2}cos\frac{��}{2}-\frac{{\sqrt{3}}}{2}$��ֵΪ$\frac{3}{5}$��
��ͼ��ԲO��x���������Ľ���ΪA����C��B��ԲO�ϣ��ҵ�Cλ�ڵ�һ���ޣ���B������Ϊ$��\frac{4}{5}��-\frac{3}{5}��$����AOC=������|BC|=1����$\sqrt{3}{cos^2}\frac{��}{2}-sin\frac{��}{2}cos\frac{��}{2}-\frac{{\sqrt{3}}}{2}$��ֵΪ$\frac{3}{5}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com