

分析 由三视图可知该几何体为四棱锥,由三视图求出几何元素的长度、判断出位置关系,利用对应的三棱柱确定外接球球心的位置,并求出球的半径,利用球的体积积公式求解.
解答 解:由三视图知该几何体为如图所示的四棱锥P-ABCD,
且PE⊥平面ABC,E、F、O分别是对应边的中点,底面ABCD是边长是4的正方形,
∵AE=ED=PE=2,∴PA⊥PD,则E是△PAD外接圆的圆心,
由图可得,四棱锥P-ABCD的外接球是直三棱柱的外接球,
∴外接球的球心是O,则OP=OC=OA=OB=OD=2$\sqrt{2}$,
∴几何体的外接球的体积S=$\frac{4}{3}π{R}^{3}$=$\frac{4}{3}$π×$(2\sqrt{2})^{3}$=$\frac{64\sqrt{2}π}{3}$.
故答案为:$\frac{64\sqrt{2}π}{3}$.
点评 本题考查了四棱锥与三棱柱的外接球的性质及其体积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,|AB|=$\sqrt{5}$,直线AB的斜率为-$\frac{1}{2}$,M是椭圆C长轴上的一个动点,设点M(m,0).
如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,|AB|=$\sqrt{5}$,直线AB的斜率为-$\frac{1}{2}$,M是椭圆C长轴上的一个动点,设点M(m,0).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
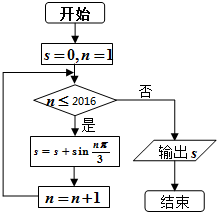
| A. | 0 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:“若y=f(x)是幂函数,则y=f(x)的图象不经过第四象限”的否命题是假命题 | |
| B. | 设a,b∈R,则“a>b”是“a|a|>b|b|”的充要条件 | |
| C. | 命题“?n∈N*,f(n)∈N*且f(n)≤n”的否定形式是“?n0∈N*,f(n0)∉N*且f(n0)≥n0” | |
| D. | 若p∨q为假命题,则p,q均为假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com