
| A. | 0 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
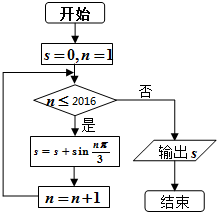
分析 根据框图的流程依次计算得到本题程序是计算S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin $\frac{2016π}{3}$的值值,根据正弦函数的性质,计算输出S的值.
解答 解:由程序框图知:本程序是计算S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin $\frac{2016π}{3}$的值,
∵y=sinx的周期是2π,
∴sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin2π=0,即一个周期内的6个数值之和为0,
由于:2016=336×6,
则S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin $\frac{2016π}{3}$=336×(sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin2π)=336×0=0.
故选:A.
点评 本题考查了循环结构的程序框图,根据框图的流程得到本程序的计算公式是解决本题的关键,要求熟练掌握三角函数的计算公式,属于基础题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x'=\frac{1}{3}x\\ y'=\frac{1}{2}y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=\frac{1}{3}x\\ y'=2y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=3x\\ y'=\frac{1}{2}y\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=3x\\ y'=2y\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
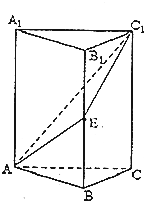 正三棱柱ABC-A1B1C1中,E为BB1的中点,AA1=2AB.
正三棱柱ABC-A1B1C1中,E为BB1的中点,AA1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
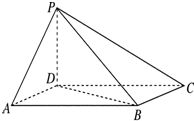 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
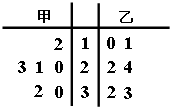 2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在
2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{3}{2}$ | C. | -$\frac{3}{2}$或0 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{{e}^{2}+1}{e}$) | B. | ($\frac{{e}^{2}+1}{e}$,+∞) | C. | $(-\frac{{{e^2}+1}}{e},-2)$ | D. | $(2,\frac{{{e^2}+1}}{e})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com