
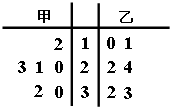
 2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在
2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ |
分析 茎叶图比较平均数和方差的大小,看叶的集中趋势,若明显,则可不计算,防止小题大做,若不明显,这计算.
解答 方法一:运动员甲的得分集中在20~30分数段的有3个,运动员乙的分数则均匀分布在10~20,20~30,30~40,个2个分数
所以估算甲的平均得分大于乙的平均得分,即${\overline{x}}_{甲}$>${\overline{x}}_{乙}$.甲分数比乙分数更集中,所以$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$
方法二:采用平均值,方差公式,计算得:
${\overline{x}}_{甲}=23$,${\overline{S}}_{甲}$=44
${\overline{x}}_{乙}=22$,${\overline{S}}_{乙}$=$\frac{245}{3}$≈81.67
故选:B
点评 本题考查由茎叶图统计平均数和方差.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,|AB|=$\sqrt{5}$,直线AB的斜率为-$\frac{1}{2}$,M是椭圆C长轴上的一个动点,设点M(m,0).
如图,A,B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,|AB|=$\sqrt{5}$,直线AB的斜率为-$\frac{1}{2}$,M是椭圆C长轴上的一个动点,设点M(m,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
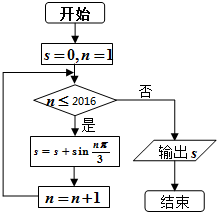
| A. | 0 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
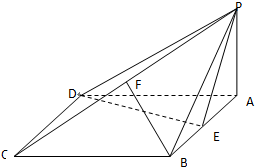 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{e}]$ | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | (-∞,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2-5i | B. | -2+5i | C. | 2+5i | D. | 2-5i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com