
分析 (Ⅰ)由题意可得:$\left\{\begin{array}{l}{m^2}=4p\\ \sqrt{4+{m^2}}=2\sqrt{3}\end{array}\right.$,求出p,即可求抛物线E的方程;
(Ⅱ)证明kGA+kGB=0,从而∠AGF=∠BGF,这表明点F到直线G A,G B的距离相等,即可证明结论.
解答 解:(I)由题意可得:$\left\{\begin{array}{l}{m^2}=4p\\ \sqrt{4+{m^2}}=2\sqrt{3}\end{array}\right.$,…(2分)
解得p=2,…(3分)
所以抛物线 E的方程为y2=4x. …(4分)
(II)因为点 A(2,m)在抛物线 E:y2=4x上,
所以$m=±2\sqrt{2}$,…(5分)
由抛物线的对称性,不妨设${A}({2,2\sqrt{2}})$.
由${A}({2,2\sqrt{2}})$,F(1,0)可得直线 AF的方程$y=2\sqrt{2}({x-1})$.…(6分)
由$\left\{\begin{array}{l}y=2\sqrt{2}({x-1})\\{y^2}=4x\end{array}\right.$,得2x2-5x+2=0,
解得x=2或$x=\frac{1}{2}$,从而${B}({\frac{1}{2},-\sqrt{2}})$. …(7分)
又G(-1,0),
所以${k_{G{A}}}=\frac{{2\sqrt{2}-0}}{{2-({-1})}}=\frac{{2\sqrt{2}}}{3}$,…(8分)${k_{G{B}}}=\frac{{-\sqrt{2}-0}}{{\frac{1}{2}-({-1})}}=-\frac{{2\sqrt{2}}}{3}$,…(9分)
所以kGA+kGB=0,从而∠AGF=∠BGF,…(10分)
这表明点F到直线G A,G B的距离相等,…(11分)
故以F为圆心且与直线G A相切的圆必与直线G B相切. …(12分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查直线与圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
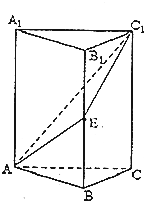 正三棱柱ABC-A1B1C1中,E为BB1的中点,AA1=2AB.
正三棱柱ABC-A1B1C1中,E为BB1的中点,AA1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
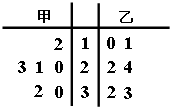 2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在
2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-2\sqrt{15}}}{10}$ | B. | $\frac{{\sqrt{5}+2\sqrt{15}}}{10}$ | C. | $\frac{{\sqrt{15}+2\sqrt{5}}}{10}$ | D. | $\frac{{\sqrt{15}-2\sqrt{5}}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com