
| A. | $\frac{{\sqrt{5}-2\sqrt{15}}}{10}$ | B. | $\frac{{\sqrt{5}+2\sqrt{15}}}{10}$ | C. | $\frac{{\sqrt{15}+2\sqrt{5}}}{10}$ | D. | $\frac{{\sqrt{15}-2\sqrt{5}}}{10}$ |
分析 利用同角三角函数的基本关系、以及三角函数在各个象限中的符号,求得sin(α-$\frac{π}{6}$) 和 cos(α-$\frac{π}{6}$)的值,再利用两角和的正弦公式求得sinα的值.
解答 解:∵α∈(-$\frac{π}{3}$,$\frac{2π}{3}$),∴α-$\frac{π}{6}$∈(-$\frac{π}{2}$,$\frac{π}{2}$),又 tan(α-$\frac{π}{6}$)=$\frac{sin(α-\frac{π}{6})}{cos(α-\frac{π}{6})}$=-2<0,
∴α-$\frac{π}{6}$∈(-$\frac{π}{2}$,0),∴sin(α-$\frac{π}{6}$)<0,cos(α-$\frac{π}{6}$)>0.
再根据 ${sin}^{2}(α-\frac{π}{6})$+${cos}^{2}(α-\frac{π}{6})$=1,可得sin(α-$\frac{π}{6}$)=-$\frac{2\sqrt{5}}{5}$,cos(α-$\frac{π}{6}$)=$\frac{\sqrt{5}}{5}$,
∴sinα=sin[(α-$\frac{π}{6}$)+$\frac{π}{6}$]=sin(α-$\frac{π}{6}$)•cos$\frac{π}{6}$+cos(α-$\frac{π}{6}$) sin$\frac{π}{6}$=-$\frac{2\sqrt{5}}{5}$•$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{5}}{5}•\frac{1}{2}$=$\frac{\sqrt{5}-2\sqrt{15}}{10}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,两角和的正弦公式的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
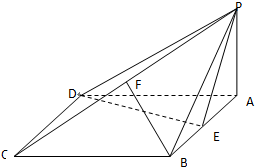 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{e}]$ | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | (-∞,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{6},0})$ | B. | $({\sqrt{2},0})$ | C. | (6,0) | D. | (2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com