
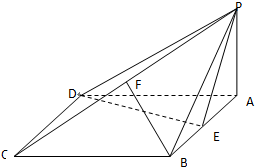
 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点. 分析 (I)证明DE⊥AB,DE⊥AP,利用线面垂直的判定定理,可得DE⊥面PAB.
(Ⅱ)证明FG与BE平行且相等,可得BF∥GE,利用线面平行的判定可得BF∥面.
解答 (本小题满分10分)
解:(Ⅰ)∵底面ABCD是菱形,∠BCD=60°,
∴△ABD为正三角形
E是AB的中点,DE⊥AB,-----------------------------------(2分)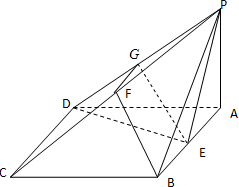
PA⊥面ABCD,DE?平面ABCD,
∴DE⊥AP,-----------------------------------(4分)
∵AP∩AB=A,
∴DE⊥平面PAB,-----------------------------------(5分)
(Ⅱ)取PD的中点G,连结FG,GE,-----------------------------------(6分)
∵F,G是中点,
∴FG∥CD且FG=$\frac{1}{2}$CD,
∴FG与BE平行且相等,
∴BF∥GE,-----------------------------------(8分)
∵GE?平面PDE,BF?平面PDE,-----------------------------------(9分)
∴BF∥面PDE.-----------------------------------(10分)
点评 本题考查线面垂直,面面垂直,考查线面平行,考查了空间想象能力和推理论证能力,正确运用判定定理是关键,属于中档题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
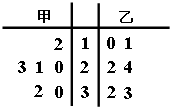 2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在
2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-2\sqrt{15}}}{10}$ | B. | $\frac{{\sqrt{5}+2\sqrt{15}}}{10}$ | C. | $\frac{{\sqrt{15}+2\sqrt{5}}}{10}$ | D. | $\frac{{\sqrt{15}-2\sqrt{5}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com