
分析 (1)直线方程按m集项,方程恒成立,得到方程组,求出点的坐标,即可证明:直线恒过定点M;
(2)可得定点Q(3,4)在直线上,由平面几何性质可得PQ⊥直线时点P到直线距离最大,由此利用垂直直线的斜率关系列式,即可解出实数m的值;
(3)若直线分别与x轴、y轴的负半轴交于A,B两点,说明直线的斜率小于0,设出斜率根据直线过的定点,写出直线方程,求出△AOB面积的表达式,利用基本不等式求出面积的最小值,即可得到面积最小值的直线的方程.
解答 (1)证明:(2+m)x+(1-2m)y+4-3m=0化为(x-2y-3)m=-2x-y-4.
由$\left\{\begin{array}{l}{x-2y-3=0}\\{-2x-y-4=0}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$
∴直线必过定点(-1,-2).
(2)解:设直线必过定点P(-1,-2).
可知点Q与定点(3,4)的连线的距离就是所求最大值,此时直线PQ与直线(2+m)x+(1-2m)y+4-3m=0垂直,
∵kPQ=$\frac{-2-4}{-1-3}$=$\frac{3}{2}$,
∴$\frac{2+m}{2m-1}$=-$\frac{2}{3}$,
解得m=-$\frac{4}{7}$,
此时,点Q(3,4)到直线的最大距离是$\sqrt{(3+1)^{2}+(4+2)^{2}}$=2$\sqrt{13}$.
综上所述,m=-$\frac{4}{7}$时,点Q(3,4)到直线的距离最大,最大值为2$\sqrt{13}$.
(3)解:设直线的斜率为k(k<0),则其方程为y+2=k(x+1),
∴OA=|$\frac{2}{k}$-1|,OB=|k-2|,
S△AOB=$\frac{1}{2}$•OA•OB=$\frac{1}{2}$|($\frac{2}{k}$-1)(k-2)|=$\frac{1}{2}$|-$\frac{(k-2)^{2}}{k}$|.
∵k<0,
∴-k>0,
∴S△AOB=$\frac{1}{2}$[-$\frac{(k-2)^{2}}{k}$]=$\frac{1}{2}$[4+(-$\frac{4}{k}$)+(-k)]≥4.
当且仅当-$\frac{4}{k}$=-k,即k=-2时取等号.
∴△AOB的面积最小值是4,
直线的方程为y+2=-2(x+1),即y+2x+4=0.(15分)
点评 本题是中档题,考查直线恒过定点的知识,三角形面积的最小值的求法,基本不等式的应用,考查计算能力,转化思想的应用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 24 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
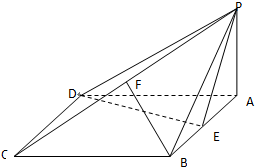 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E 是AB的中点,F是PC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{e}]$ | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | (-∞,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2$\sqrt{2}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点$(2,\sqrt{3})$,且它的离心率e=$\frac{1}{2}$.直线l:y=kx+t与椭圆C1交于M、N两点.
已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点$(2,\sqrt{3})$,且它的离心率e=$\frac{1}{2}$.直线l:y=kx+t与椭圆C1交于M、N两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com