
| A. | $(-∞,\frac{1}{e}]$ | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | (-∞,e) |
分析 若?x0∈(0,+∞),不等式ax-lnx<0成立,则?x0∈(0,+∞),不等式a<$\frac{lnx}{x}$成立,令f(x)=$\frac{lnx}{x}$,则a<f(x)max,利用导数法,求出函数的最大值,可得答案.
解答 解:若?x0∈(0,+∞),不等式ax-lnx<0成立,
则?x0∈(0,+∞),不等式a<$\frac{lnx}{x}$成立,
令f(x)=$\frac{lnx}{x}$,则a<f(x)max,
∵f′(x)=$\frac{1-lnx}{{x}^{2}}$,
则x∈(0,e)时,f′(x)>0,f(x)=$\frac{lnx}{x}$为增函数,
x∈(e,+∞)时,f′(x)<0,f(x)=$\frac{lnx}{x}$为减函数,
故x=e时,f(x)max=$\frac{1}{e}$,
故a的取值范围是$(-∞,\frac{1}{e})$,
故选:C
点评 本题以命题的真假判断与应用为载体,考查了存在性问题,利用导数求函数的最值,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
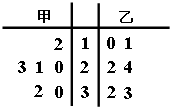 2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在
2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4:2战胜辽宁药都队卫冕成功.如图是参加此次总决赛的甲、乙两名运动员在| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$>$\overline{{S}_{乙}}$ | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,$\overline{{S}_{甲}}$<$\overline{{S}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-2\sqrt{15}}}{10}$ | B. | $\frac{{\sqrt{5}+2\sqrt{15}}}{10}$ | C. | $\frac{{\sqrt{15}+2\sqrt{5}}}{10}$ | D. | $\frac{{\sqrt{15}-2\sqrt{5}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
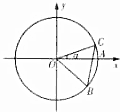 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为$(\frac{4}{5},-\frac{3}{5})$,∠AOC=α,若|BC|=1,则$\sqrt{3}{cos^2}\frac{α}{2}-sin\frac{α}{2}cos\frac{α}{2}-\frac{{\sqrt{3}}}{2}$的值为$\frac{3}{5}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为$(\frac{4}{5},-\frac{3}{5})$,∠AOC=α,若|BC|=1,则$\sqrt{3}{cos^2}\frac{α}{2}-sin\frac{α}{2}cos\frac{α}{2}-\frac{{\sqrt{3}}}{2}$的值为$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com