
分析 (1)利用递推关系与等差数列的通项公式即可得出.
(2)利用分组求和、“裂项求和”方法、“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)∵${S_n}=n{a_n}+\frac{1}{2}n({n-1})$①,
∴${S_{n+1}}=({n+1}){a_{n+1}}+\frac{1}{2}({n+1})n$②,
②-①得,an+1=(n+1)an+1-nan+n,
∴an+1-an=-1,
∴an=0+(n-1)×(-1)=1-n.
(2)由(1)知${b_n}=\left\{\begin{array}{l}n•{2^{1-n}},n=2k-1\\ \frac{1}{{{n^2}+2n}},n=2k\end{array}\right.({k∈{{N}^*}})$,
∴T2n=b1+b2+b3+…+b2n=[1×20+3×2-2+5×2-4+…+(2n-1)•22-2n]+$\frac{1}{2}({\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+…+\frac{1}{2n}-\frac{1}{2n+2}})$=$[{1×{2^0}+3×{2^{-2}}+5×{2^{-4}}+…+({2n-1})•{2^{2-2n}}}]+\frac{n}{{4({n+1})}}$,
设A=1×20+3×2-2+5×2-4+…+(2n-1)•22-2n,
则2-2A=1×2-2+3×2-4+5×2-6+…+(2n-3)•22-2n+(2n-1)•2-2n,
两式相减得$\frac{3}{4}A=1+2({{2^{-2}}+{2^{-4}}+{2^{-6}}+…+{2^{2-2n}}})-({2n-1})•{2^{-2n}}$,
整理得$A=\frac{20}{9}-\frac{24n+20}{{9×{2^{2n}}}}$,
∴${T_{2n}}=\frac{20}{9}-\frac{24n+20}{{9×{2^{2n}}}}+\frac{n}{{4({n+1})}}$.
点评 本题考查了递推关系、分组求和方法、“裂项求和”方法、“错位相减法”、等差数列与等比数列的求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{e}]$ | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | (-∞,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2-5i | B. | -2+5i | C. | 2+5i | D. | 2-5i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{6},0})$ | B. | $({\sqrt{2},0})$ | C. | (6,0) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点$(2,\sqrt{3})$,且它的离心率e=$\frac{1}{2}$.直线l:y=kx+t与椭圆C1交于M、N两点.
已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点$(2,\sqrt{3})$,且它的离心率e=$\frac{1}{2}$.直线l:y=kx+t与椭圆C1交于M、N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
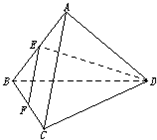 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com