
 ijУ���Ա�У�����Ŀ�ѧ����һ��ģ�⿼�Ե���ѧ�ɼ����з������÷ֲ����������ȡ��20��ѧ���ijɼ��������þ�Ҷͼ��¼��ͼ��ʾ���������ݶ�ʧ��������������Ƶ�ʷֲ�����
ijУ���Ա�У�����Ŀ�ѧ����һ��ģ�⿼�Ե���ѧ�ɼ����з������÷ֲ����������ȡ��20��ѧ���ijɼ��������þ�Ҷͼ��¼��ͼ��ʾ���������ݶ�ʧ��������������Ƶ�ʷֲ�����| �����Σ��֣� | [50��70�� | [70��90�� | [90��110�� | [110��130�� | [130��150] | �ϼ� |
| Ƶ�� | b | |||||
| Ƶ�� | a | 0.2 |
���� ��1���ɾ�Ҷͼ��֪������[50��70����Χ�ڵ���3�ˣ���[130��150]��Χ�ڵ���2�ˣ��ɴ����������a��b��ֵ��������[70��80����[90��100����Χ�ڵ�ѧ��������
��2�����¼�A��ʾ���Ӵ��ڵ���120�ֵ�ѧ�������ѡ2��ѧ���÷֣�����ȡ��һ��ѧ���÷���[130��150]�����ɾ�Ҷͼ��֪���ڵ���120����5�ˣ������оٷ����������ȡ��һ��ѧ���÷���[130��150]�ĸ��ʣ�
��� �⣺��1���ɾ�Ҷͼ��֪������[50��70����Χ�ڵ���3�ˣ�
��[130��150]��Χ�ڵ���2�ˣ�
��a=$\frac{3}{20}$=0.15��b=2����2�֣�
�ַ�����[70��90����Χ�ڵ�Ƶ��Ϊ0.2��
�������[70��90����Χ�ڵ�����Ϊ20��0.2=4��
�������[70��80����Χ�ڵ�����Ϊ1����4�֣�
�������[90��100����Χ�ڵ�ѧ����Ϊ20-16=4���ˣ�����6�֣�
��2�����¼�A��ʾ���Ӵ��ڵ���120�ֵ�ѧ�������ѡ2��ѧ���÷֣�
����ȡ��һ��ѧ���÷���[130��150]����
�ɾ�Ҷͼ��֪���ڵ���120����5�ˣ�
����5�˷����ֱ�Ϊ121��124��128��138��144��
��ѡȡѧ�����������п��ܽ��Ϊ��
��121��124������121��128������121��138������121��144����
��124��128������124��138������124��144������128��138����
��128��144������138��144��������10�������¼�����9�֣�
�¼�A�Ŀ��ܽ��Ϊ����121��138������121��144������124��138������124��144����
��128��138������128��144������138��144����7�������
��������ȡ��һ��ѧ���÷���[130��150]�ĸ���p=$\frac{7}{10}$����12�֣�
���� ���⿼�龥Ҷͼ��Ƶ�ʷֲ�����Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
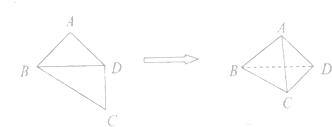
| A�� | $\frac{8\sqrt{2}}{3}$�� | B�� | 24�� | C�� | 4$\sqrt{3}$�� | D�� | 12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
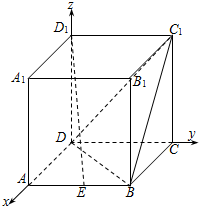 ��֪������ABCD-A1B1C1D1���ⳤΪ2����EΪ��AB���е㣮
��֪������ABCD-A1B1C1D1���ⳤΪ2����EΪ��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2\sqrt{3}}{3}$ | B�� | $\frac{2\sqrt{3}}{3}$ | C�� | $\frac{5}{3}$ | D�� | -$\frac{5}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ | B�� | ƽ�� | C�� | ��ƽ����� | D�� | ƽ�л���ƽ����� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com