
 AED沿AE折起到
AED沿AE折起到 的位
的位 置时,有平面
置时,有平面
 平面ABCE,
平面ABCE,

 (如图)
(如图) 求点D/到平面ABCE的距离.
求点D/到平面ABCE的距离.
 ,由BD
,由BD AC,且平面ACD
AC,且平面ACD
 平面ABCE于AC,∴BD
平面ABCE于AC,∴BD 平面ACD
平面ACD ,故C
,故C D
D
 BD,又CD
BD,又CD
 BD
BD ,∴CD
,∴CD
 平面BDD
平面BDD ,即得CD
,即得CD
 DD
DD ,在Rt△CDD
,在Rt△CDD 中,由于ED=ED
中,由于ED=ED ,∴∠EDD
,∴∠EDD =∠ED
=∠ED D,
D, =900
=900 EDD
EDD =900
=900 ED
ED D=∠ED
D=∠ED C,∴EC=ED
C,∴EC=ED =ED,
=ED, (II)方法一:如图取OC的中
(II)方法一:如图取OC的中 点M,连结D
点M,连结D M、EM,
M、EM, 平面ACD
平面ACD ,
, =900,又因为D
=900,又因为D E=2,EM
E=2,EM =
= ,
, M=
M= ,又AD
,又AD
 EM,∵AD
EM,∵AD DE,
DE,
 D
D E,∴AD
E,∴AD
 平
平 面EMD
面EMD ,
,
 D
D M,在Rt△AMD
M,在Rt△AMD 中,AD
中,AD =4,AM=
=4,AM= ,D
,D M=
M= ,
, 作D
作D H
H AM于H点,则D
AM于H点,则D H
H 平面ABCE,
平面ABCE, H=
H= ,此即得点D
,此即得点D 到平面ABCE的距离.
到平面ABCE的距离.  方法二:如图, 连结OD
方法二:如图, 连结OD ,∵CD
,∵CD
 平面BDD
平面BDD ,
, 
 OD
OD ,
, C中,设OD
C中,设OD
 ,
, ,∴CD
,∴CD =
= ,
, 与∠D
与∠D OC互补,
OC互补, ,
, ,在直角三角形OD
,在直角三角形OD C中,
C中,  面积公式得所求距离为
面积公式得所求距离为 .
. 方法三:能用最小角定理
方法三:能用最小角定理 帮助解△AD
帮助解△AD C,
C, ,其中
,其中
 ,0),D
,0),D (
( ),
), H
H 平面ABCE于H点,则H在AC上,
平面ABCE于H点,则H在AC上, ,0),依题意有:
,0),依题意有: ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,∴
,∴ ,
, ,∴
,∴
 与
与 两式相减,
两式相减, 代入得
代入得 ,从而有
,从而有 ,
, 中点,点D
中点,点D 到平面ABCE的距离是
到平面ABCE的距离是 . …………………12分
. …………………12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 X∥Y”为真命题的是_________(填序号)
X∥Y”为真命题的是_________(填序号)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
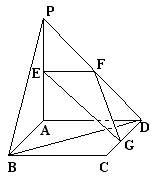
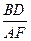 为何值时,平面DEF
为何值时,平面DEF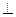 平面BEF?并证明你的结论。(8分)
平面BEF?并证明你的结论。(8分)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com