
分析 (1)设点P的坐标为(x,y),a=5,b=3时,c=$\sqrt{{a}^{2}-{b}^{2}}$,F1(-4,0),由P(x,y)在椭圆上,可得:${y}^{2}=9(1-\frac{{x}^{2}}{25})$.代入可得$|{\overrightarrow{{F_1}P}}$|=$\sqrt{(x+4)^{2}+{y}^{2}}$=$\sqrt{(\frac{4}{5}x+5)^{2}}$,由-5≤x≤5,可知:$\frac{4}{5}x+5$>0,可得$|\overrightarrow{{F}_{1}P}|$.
(2)设点T的坐标为(x,y),分类讨论:当$|\overrightarrow{PT}|$=0时,点(a,0)和点(-a,0)在轨迹上,当$|\overrightarrow{PT}|$≠0,且$|\overrightarrow{T{F}_{2}}|$≠0时,由$\overrightarrow{PT}•\overrightarrow{T{F_2}}$=0,可得$\overrightarrow{PT}$⊥$\overrightarrow{T{F}_{2}}$.又$|\overrightarrow{PQ}|$=$|\overrightarrow{P{F}_{2}}|$,可得T为线段F2Q的中点.在△QF1F2中,|OT|=$\frac{1}{2}$|F1Q|=a,即可得出.
(3)C上存在点M(x0,y0)使S=b2的充要条件是$\left\{\begin{array}{l}{{x}_{0}^{2}+{y}_{0}^{2}={a}^{2}}\\{\frac{1}{2}•2c•|{y}_{0}|={b}^{2}}\end{array}\right.$,可得|y0|≤a,|y0|=$\frac{{b}^{2}}{c}$,当$a≥\frac{{b}^{2}}{c}$时,存在点M,使S=b2;利用数量积运算性质与三角形面积计算公式即可得出.
解答 解:(1)设点P的坐标为(x,y),a=5,b=3时,c=$\sqrt{{a}^{2}-{b}^{2}}$=4,∴F1(-4,0),由P(x,y)在椭圆上,∴${y}^{2}=9(1-\frac{{x}^{2}}{25})$.
得$|{\overrightarrow{{F_1}P}}$|=$\sqrt{(x+4)^{2}+{y}^{2}}$=$\sqrt{(x+4)^{2}+9(1-\frac{{x}^{2}}{25})^{2}}$=$\sqrt{(\frac{4}{5}x+5)^{2}}$,∵-5≤x≤5,可知:$\frac{4}{5}x+5$>0,∴$|\overrightarrow{{F}_{1}P}|$=$\frac{4}{5}x+5$.
(2)设点T的坐标为(x,y),
当$|\overrightarrow{PT}|$=0时,点(a,0)和点(-a,0)在轨迹上,
当$|\overrightarrow{PT}|$≠0,且$|\overrightarrow{T{F}_{2}}|$≠0时,由$\overrightarrow{PT}•\overrightarrow{T{F_2}}$=0,可得$\overrightarrow{PT}$⊥$\overrightarrow{T{F}_{2}}$.
又$|\overrightarrow{PQ}|$=$|\overrightarrow{P{F}_{2}}|$,∴T为线段F2Q的中点.
在△QF1F2中,|OT|=$\frac{1}{2}$|F1Q|=a,∴x2+y2=a2.
综上所述,点T的轨迹C的方程是:x2+y2=a2.
(3)C上存在点M(x0,y0)使S=b2的充要条件是$\left\{\begin{array}{l}{{x}_{0}^{2}+{y}_{0}^{2}={a}^{2}}\\{\frac{1}{2}•2c•|{y}_{0}|={b}^{2}}\end{array}\right.$,
可得|y0|≤a,|y0|=$\frac{{b}^{2}}{c}$,当$a≥\frac{{b}^{2}}{c}$时,存在点M,使S=b2;
当$a<\frac{{b}^{2}}{c}$时,不存在满足条件的点M.
当$a≥\frac{{b}^{2}}{c}$时,$\overrightarrow{M{F}_{1}}$=(-c-x0,-y0),$\overrightarrow{M{F}_{2}}$=(c-x0,-y0),
由$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=${x}_{0}^{2}$-c2+${y}_{0}^{2}$=a2-c2=b2,
由$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=$|\overrightarrow{M{F}_{1}}|$$|\overrightarrow{M{F}_{2}}|$cos∠F1MF2,
S=$\frac{1}{2}$$|\overrightarrow{M{F}_{1}}|$$|\overrightarrow{M{F}_{2}}|$sin∠F1MF2=b2,
可得:tan∠F1MF2=2.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、数量积运算性质、线段的垂直平分线的性质、三角形面积计算公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | (0,e) | C. | ($\frac{1}{e}$,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
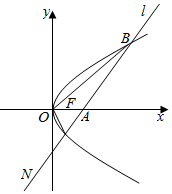 如图,已知抛物线C以坐标原点O为顶点,焦点F在x轴的正半轴上,且|OF|=$\frac{1}{2}$.
如图,已知抛物线C以坐标原点O为顶点,焦点F在x轴的正半轴上,且|OF|=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
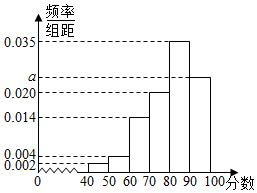 2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
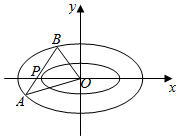 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1的离心率e=$\frac{1}{2}$,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1的离心率e=$\frac{1}{2}$,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com