
分析 (1)由题意可知,弦长为直径的圆的面积最小,由垂径定理求出半弦长,就是最小的圆的半径,再联立直线方程和圆的方程,利益根与系数的关系求出圆心坐标,即可求得面积最小的圆的方程;
(2)设出设经过直线l:2x+y+4=0和圆C:x2+y2+2x-4y+1=0的圆系方程,代入已知点的坐标求得λ,则圆的方程可求.
解答 解:(1)∵圆x2+y2+2x-4y+1=0的方程可化为(x+1)2+(y-2)2=4.
∴圆心坐标为(-1,2),半径为r=2;
∴圆心到直线2x+y+4=0的距离为d=$\frac{|-2+2+4|}{\sqrt{5}}=\frac{4}{\sqrt{5}}$.
设直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点为A,B.则|AB|=2$\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{4-(\frac{4}{\sqrt{5}})^{2}}=\frac{4}{\sqrt{5}}$.
∴过点A,B的最小圆半径为$\frac{2}{\sqrt{5}}$.
联立$\left\{\begin{array}{l}{2x+y+4=0}\\{{x}^{2}+{y}^{2}+2x-4y+1=0}\end{array}\right.$,得5x2+26x+33=0,
故${x}_{1}+{x}_{2}=-\frac{26}{5}$,则圆心的横坐标为$-\frac{13}{5}$,纵坐标为2×(-$\frac{13}{5}$)-4=$-\frac{46}{5}$,
∴最小圆的圆心为(-$\frac{13}{5}$,$-\frac{46}{5}$),
∴最小圆的方程为(x+$\frac{13}{5}$)2+(y+$\frac{46}{5}$)2=$\frac{4}{5}$;
(2)设经过直线l:2x+y+4=0和圆C:x2+y2+2x-4y+1=0的交点的圆的方程为x2+y2+2x-4y+1+λ(2x+y+4)=0.
∵点(2,-1)在圆上,∴22+(-1)2+2×2-4×(-1)+1+λ(4-1+4)=0,
解得:λ=-2.
∴所求圆的方程为:x2+y2+2x-4y+1+-2(2x+y+4)=0.
即x2+y2-2x-6y-7=0.
点评 本题考查的知识点是直线与圆的位置关系,考查数学转化思想方法,训练了圆系方程的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
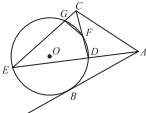 如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.
如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不是充分条件也不是必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com