
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
| 2 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
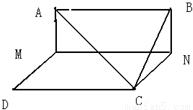
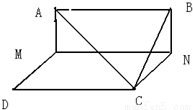
 如图,边长为3正方形ABCD,动点M,N在AD,BC上,且MN∥CD,沿MN将正方形折成直二面角,设AM=x,则点M到平面ABC的距离的最大值为( )
如图,边长为3正方形ABCD,动点M,N在AD,BC上,且MN∥CD,沿MN将正方形折成直二面角,设AM=x,则点M到平面ABC的距离的最大值为( )查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建泉州五中、莆田、漳州一中高三上期末理数学卷(解析版) 题型:解答题
如图, 是边长为
是边长为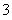 的正方形,
的正方形,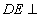 平面
平面 ,
,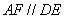 ,
,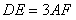 ,
,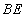 与平面
与平面 所成角为
所成角为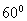 .
.
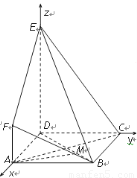
(1)求证: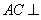 平面
平面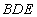 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)设点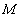 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得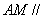 平面
平面 ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆八中高三(下)第二次月考数学试卷(文科)(解析版) 题型:选择题
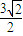
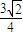
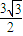
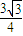
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com