
已知函数![]() ,
,![]() 。
。
(I)当函数![]() 取得最大值时,求自变量
取得最大值时,求自变量![]() 的集合;
的集合;
(II)该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换
的图象经过怎样的平移和伸缩变换
得到?
本小题主要考查三角函数的图象和性质、利用三角公式进行恒等变形的技能以及运算能力.
解:
(Ⅰ)y=![]() sinx+cosx
sinx+cosx
=2(sinxcos![]() +cosxsin
+cosxsin![]() )=2sin(x+
)=2sin(x+![]() ),x∈R.
),x∈R.
y取得最大值必须且只需x+![]() =
=![]() +2kπ,k∈Z,
+2kπ,k∈Z,
即 x=![]() +2kπ,k∈Z.
+2kπ,k∈Z.
所以,当函数y取得最大值时,自变量x的集合为|x|x=![]() +2 kπ,k∈Z|.
+2 kπ,k∈Z|.
(Ⅱ)变换的步骤是:
(1)把函数y=sinx的图象向左平移![]() ,得到函数y=sin(x+
,得到函数y=sin(x+![]() )的图象;
)的图象;
(2)令所得到的图象上各点横坐标不变,把纵坐标伸长到原来的2倍,得到函数
y=2sin(x+![]() )的图象;
)的图象;
经过这样的变换就得到函数y=![]() sinx+cosx的图象.
sinx+cosx的图象.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
(07年辽宁卷理)(12分)
已知函数![]() ,
,![]() .
.
(I)证明:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(II)对于给定的闭区间![]() ,试说明存在实数
,试说明存在实数![]() ,当
,当![]() 时,
时,![]() 在闭区间
在闭区间![]() 上是减函数;
上是减函数;
(III)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省十校联合体高三(上)期初联考数学试卷 (理科)(解析版) 题型:解答题
 ,
, .
.查看答案和解析>>
科目:高中数学 来源:2010年高考试题(福建卷)解析版(理) 题型:解答题
(Ⅰ)已知函数 ,
, 。
。
(i)求函数 的单调区间;
的单调区间;
(ii)证明:若对于任意非零实数 ,曲线C与其在点
,曲线C与其在点 处的切线交于另一点
处的切线交于另一点
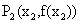 ,曲线C与其在点
,曲线C与其在点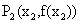 处的切线交于另一点
处的切线交于另一点 ,线段
,线段

(Ⅱ)对于一般的三次函数 (Ⅰ)(ii)的正确命题,并予以证明。
(Ⅰ)(ii)的正确命题,并予以证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com