
已知集合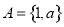 ,
, ,则“
,则“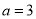 ”是“
”是“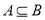 ”的( )
”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
A.
【解析】
试题解析:若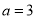 ,则
,则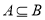 ;若
;若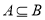 ,则
,则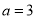 或
或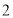 ,所以“
,所以“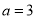 ”是“
”是“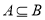 ”的充分而不必要条件,故选A
”的充分而不必要条件,故选A
考点:集合间的关系,充分必要条件
考点分析: 考点1:必要条件、充分条件与充要条件的判断 【知识点的认识】正确理解和判断充分条件、必要条件、充要条件和非充分非必要以及原命题、逆命题否命题、逆否命题的概念是本节的重点;掌握逻辑推理能力和语言互译能力,对充要条件概念本质的把握是本节的难点.

科目:高中数学 来源:2014-2015学年山东青岛平度市三校高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知向量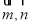 分别是直线
分别是直线 和平面
和平面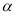 的方向向量和法向量,若
的方向向量和法向量,若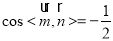 ,则
,则 与
与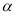 所成的角为( )
所成的角为( )
A.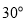 B.
B.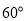 C.
C.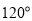 D.
D.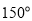
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省高二上学期期末考试数学试卷(解析版) 题型:选择题
设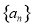 是等比数列,
是等比数列,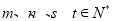 ,则“
,则“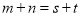 ”是“
”是“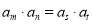 ”的( )
”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省新余市高一上学期期末考试数学试卷(解析版) 题型:填空题
对于四面体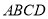 ,以下说法中,正确的序号为 (多选、少选、选错均不得分).
,以下说法中,正确的序号为 (多选、少选、选错均不得分).
①若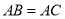 ,
,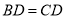 ,
,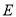 为
为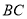 中点,则平面
中点,则平面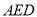 ⊥平面
⊥平面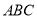 ;
;
②若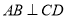 ,
,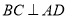 ,则
,则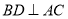 ;
;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以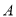 为端点的三条棱所在直线两两垂直,则
为端点的三条棱所在直线两两垂直,则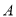 在平面
在平面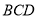 内的射影为
内的射影为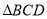 的垂心;
的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分12分)已知向量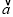 =
=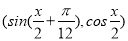 ,
,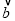 =
=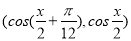 ,
,
x∈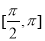 ,设函数
,设函数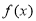 =
=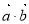 .
.
(1)若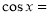 -
-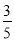 ,求函数f(x)的值;
,求函数f(x)的值;
(2)将函数f(x)的图象先向右平移m个单位,再向上平移n个单位,使平移后的图象
关于原点对称,若0<m<π,n>0,试求6m+2n的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
下列说法中正确的是( )
A.命题“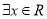 ,使得
,使得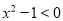 ”的否定是“
”的否定是“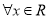 ,均有
,均有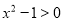 ”;
”;
B.命题“若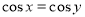 ,则x=y”的逆否命题是真命题:
,则x=y”的逆否命题是真命题:
C.命题“若x=3,则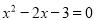 ”的否命题是“若
”的否命题是“若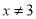 ,则
,则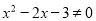 ”;
”;
D.命题“存在四边相等的四边形不是正方形”是假命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com