
下面是判断
n是否是一个质数的程序,运算次数比较多,结构也比较复杂,例50中,d≤n-1,按质数的定义,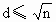 即可,这是什么原因?你觉得
即可,这是什么原因?你觉得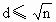 这改法好不好?有没有更好的办法,其他步骤有没有更改的地方,不妨给出你的程序?
这改法好不好?有没有更好的办法,其他步骤有没有更改的地方,不妨给出你的程序?
|
10 |
INPUT “n=”;n |
|
20 |
flag=1 |
|
30 |
IF n>2 THEN |
|
40 |
d=2 |
|
50 |
WHILE d<=n-1 AND flag=1 |
|
60 |
IF n MOD d=0 THEN |
|
70 |
Flag=0 |
|
80 |
ELSE |
|
90 |
d=d+1 |
|
100 |
END IF |
|
110 |
WEND |
|
120 |
ELSE |
|
130 |
IF flag=1 THEN |
|
140 |
PRINT n;“是质数.” |
|
150 |
ELSE |
|
160 |
PRINT n;“不是质数.” |
|
170 |
END IF |
|
180 |
END IF |
|
190 |
END |
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
| x |
| 3 |
| cosx |
| 4 |
| 1 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模理)(13分)
设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;
有实数根;
②函数![]() 的导数
的导数![]() 满足
满足![]() ”
”
(I)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
查看答案和解析>>
科目:高中数学 来源: 题型:
①终端框(起止框),表示一个算法的起始和结束 ②输入、输出框,表示一个算法输入和输出的信息 ③处理框(执行框),功能是赋值、计算 ④判断框,判断某一条件是否成立,成立时在出口处标明“是”或“Y”,不成立时标明“否”或“N”
A.(1)与①,(2)与②,(3)与③,(4)与④
B.(1)与④,(2)与②,(3)与①,(4)与③
C.(1)与①,(2)与③,(3)与②,(4)与④
D.(1)与①,(2)与③,(3)与④,(4)与②
查看答案和解析>>
科目:高中数学 来源: 题型:
设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]()
![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() .”
.”
(I)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意
[m,n]![]() D,都存在
D,都存在![]()
![]() [m,n],使得等式
[m,n],使得等式![]() 成立”,
成立”,
试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(III)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() .
.
查看答案和解析>>
科目:高中数学 来源:广东省模拟题 题型:解答题
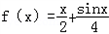 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;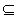 D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.试用这一性质证明:方程f(x)﹣x=0只有一个实数根;
D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.试用这一性质证明:方程f(x)﹣x=0只有一个实数根;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com