
【题目】定义:若函数y=f(x)在某一区间D上任取两个实数x1、x2 , 且x1≠x2 , 都有 ![]() ,则称函数y=f(x)在区间D上具有性质L.
,则称函数y=f(x)在区间D上具有性质L.
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)对于函数 ![]() ,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
(3)若函数 ![]() 在区间(0,1)上具有性质L,求实数a的取值范围.
在区间(0,1)上具有性质L,求实数a的取值范围.
【答案】
(1)解: ![]() (或其它底在(0,1)上的对数函数)
(或其它底在(0,1)上的对数函数)
(2)解:函数 ![]() 在区间(0,+∞)上具有性质L.
在区间(0,+∞)上具有性质L.
证明:任取x1、x2∈(0,+∞),且x1≠x2
则 ![]() =
= ![]() =
= ![]()
∵x1、x2∈(0,+∞)且x1≠x2,
∴(x1﹣x2)2>0,2x1x2(x1+x2)>0
即 ![]() >0,
>0,
∴ ![]()
所以函数 ![]() 在区间(0,+∞)上具有性质L
在区间(0,+∞)上具有性质L
(3)解:任取x1、x2∈(0,1),且x1≠x2
则 ![]() =
= ![]() =
= ![]() =
= ![]()
∵x1、x2∈(0,1)且x1≠x2,
∴(x1﹣x2)2>0,4x1x2(x1+x2)>0
要使上式大于零,必须2﹣ax1x2(x1+x2)>0在x1、x2∈(0,1)上恒成立,
即 ![]() ,
,
∴a≤1,
即实数a的取值范围为(﹣∞,1]
【解析】(1)写出的函数是下凹的函数即可;(2)函数 ![]() 在区间(0,+∞)上具有性质L.根据定义,任取x1、x2∈(0,+∞),且x1≠x2
在区间(0,+∞)上具有性质L.根据定义,任取x1、x2∈(0,+∞),且x1≠x2
只需要证明 ![]() >0即可;(3)任取x1、x2∈(0,1),且x1≠x2则
>0即可;(3)任取x1、x2∈(0,1),且x1≠x2则 ![]() >0,只需要2﹣ax1x2(x1+x2)>0在x1、x2∈(0,1)上恒成立,即
>0,只需要2﹣ax1x2(x1+x2)>0在x1、x2∈(0,1)上恒成立,即 ![]() ,故可求实数a的取值范围.
,故可求实数a的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
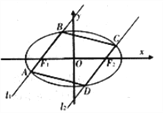
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,![]() ,
,![]() =4 ,
=4 ,![]() ,F为棱AE的中点.
,F为棱AE的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在探究实系数一元二次方程的根与系数的关系时,可按下述方法进行:
设实系数一元二次方程![]() ……①
……①
在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,则方程①可变形为
,则方程①可变形为![]() ,
,
展开得![]() .……②
.……②
比较①②可以得到: 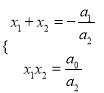
类比上述方法,设实系数一元![]() 次方程
次方程![]() (
(![]() 且
且![]() )在复数集
)在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,…,
,…, ![]() ,则这
,则这![]() 个根的积
个根的积![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)= ![]() ﹣1(x∈R)时,得出了下面4个结论:①等式f(﹣x)=f(x)在x∈R时恒成立;②函数f(x)在x∈R上的值域为(﹣1,1];③曲线y=f(x)与g(x)=2x﹣2仅有一个公共点;④若f(x)=
﹣1(x∈R)时,得出了下面4个结论:①等式f(﹣x)=f(x)在x∈R时恒成立;②函数f(x)在x∈R上的值域为(﹣1,1];③曲线y=f(x)与g(x)=2x﹣2仅有一个公共点;④若f(x)= ![]() ﹣1在区间[a,b](a,b为整数)上的值域是[0,1],则满足条件的整数数对(a,b)共有5对.其中正确结论的序号有(请将你认为正确的结论的序号都填上).
﹣1在区间[a,b](a,b为整数)上的值域是[0,1],则满足条件的整数数对(a,b)共有5对.其中正确结论的序号有(请将你认为正确的结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
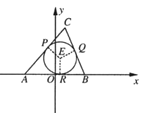
【题目】已知△ABC的两顶点坐标A(﹣1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M.
(I)求曲线M的方程;
(Ⅱ)设直线BC与曲线M的另一交点为D,当点A在以线段CD为直径的圆上时,求直线BC的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com