
【题目】在探究实系数一元二次方程的根与系数的关系时,可按下述方法进行:
设实系数一元二次方程![]() ……①
……①
在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,则方程①可变形为
,则方程①可变形为![]() ,
,
展开得![]() .……②
.……②
比较①②可以得到: 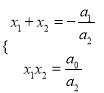
类比上述方法,设实系数一元![]() 次方程
次方程![]() (
(![]() 且
且![]() )在复数集
)在复数集![]() 内的根为
内的根为![]() ,
, ![]() ,…,
,…, ![]() ,则这
,则这![]() 个根的积
个根的积![]() __________.
__________.
科目:高中数学 来源: 题型:
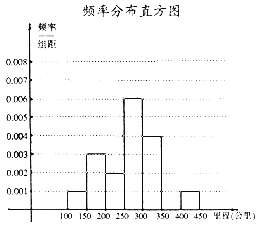
【题目】面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
频率分布表
分组 | 频数 | 频率 |
[100,150) | 1 | 0.05 |
[150,200) | 3 | 0.15 |
[200,250) | x | 0.1 |
[250,300) | 6 | 0.3 |
[300,350) | 4 | 0.2 |
[350,400) | 3 | y |
[400,450] | 1 | 0.05 |
合计 | N | 1 |
(1)试确定频率分布表中x,y,N的值,并补全频率分布直方图;
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行节日促销活动,消费满一定数额即可获得一次抽奖机会,抽奖这可以从以下两种方式中任选一种进行抽奖.
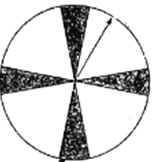
抽奖方式①:让抽奖者随意转动如图所示的圆盘,圆盘停止后指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即中奖.
,边界忽略不计)即中奖.
抽奖方式②:让抽奖者从装有3个白球和3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即中奖.
假如你是抽奖者,为了让中奖的可能性大,你应该选择哪一种抽奖方式?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且当x≥0时, ![]() ,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,设点
,设点![]() ,且
,且![]() =2.
=2.
(1)求椭圆C的方程;
(2)已知四边形MNPQ的四个顶点均在曲线C上,且MQ∥NP,MQ⊥x轴,若直线MN和直线QP交于点S(4,0).判断四边形MNPQ两条对角线的交点是否为定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数y=f(x)在某一区间D上任取两个实数x1、x2 , 且x1≠x2 , 都有 ![]() ,则称函数y=f(x)在区间D上具有性质L.
,则称函数y=f(x)在区间D上具有性质L.
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)对于函数 ![]() ,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
(3)若函数 ![]() 在区间(0,1)上具有性质L,求实数a的取值范围.
在区间(0,1)上具有性质L,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:(1)函数f(x)在[0,+∞)上是增函数,在(﹣∞,0)上也是增函数,所以f(x)在R上是增函数;(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0,且a>0; (3)y=x2﹣2|x|﹣3的递增区间为[1,+∞);(4)函数y=lg10x和函数y=elnx表示相同函数.其中正确命题的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,记函数f(x)=a ![]() +
+ ![]() +
+ ![]() 的最大值为g(a).
的最大值为g(a).
(1)设t= ![]() +
+ ![]() ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);
(2)求g(a);
(3)试求满足g(a)=g( ![]() )的所有实数a.
)的所有实数a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com