
 ,则f(x+π)=f(x)对?x∈R恒成立.
,则f(x+π)=f(x)对?x∈R恒成立. 为非零向量,且
为非零向量,且 ,则
,则
 的图象,只需将函数
的图象,只需将函数 的图象向右平移
的图象向右平移 个单位,其中真命题的有 .
个单位,其中真命题的有 . 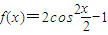 =2cosx,
=2cosx,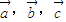 为非零向量,
为非零向量,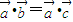 ,则
,则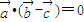
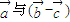 垂直,不一定
垂直,不一定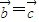 .故(3)错误
.故(3)错误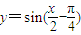 的图象向右平移
的图象向右平移 个单位,
个单位,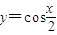 的图象,故(4)错误
的图象,故(4)错误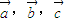 为非零向量,若
为非零向量,若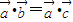 ,则
,则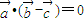
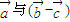 垂直,不一定
垂直,不一定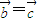 .大家一定要注意,另外三个向量相乘还不满足乘法的结合律,这是向量运算中的另一个易忽略点.
.大家一定要注意,另外三个向量相乘还不满足乘法的结合律,这是向量运算中的另一个易忽略点. 

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| x |
| 2 |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| x |
| 2 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:巢湖模拟 题型:填空题
| x |
| 2 |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| x |
| 2 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题中
(1)若四点中任何三点都不共线,则这四点不共面;
(2)在空间,两条直线没有公共点是这两条直线平行的充分不必要条件;
(3)若直线![]() 与平面
与平面![]() 、
、![]() 满足条件:
满足条件:![]() 且
且![]() ,则
,则![]() ;
;
(4)底面为矩形,且有两个侧面是矩形的平行六面体是长方体。
其中真命题的个数为( )
![]() 1个
1个 ![]() 2个
2个 ![]() 3个
3个 ![]() 4
4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com