
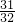 ,则S△ABC=
,则S△ABC=

 ,可得 sinC 的值,再根据S△ABC=
,可得 sinC 的值,再根据S△ABC= •a•b•sinC,运算求得结果.
•a•b•sinC,运算求得结果.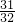 ,由余弦定理得:(5-x)2=x2+16-8x•cos(B-A),
,由余弦定理得:(5-x)2=x2+16-8x•cos(B-A), ,∴sinC=
,∴sinC=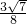 .
. •a•b•sinC=
•a•b•sinC= ×4×5×
×4×5×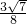 =
= ,
, ,是解题的关键,属于中档题.
,是解题的关键,属于中档题. 

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com