
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.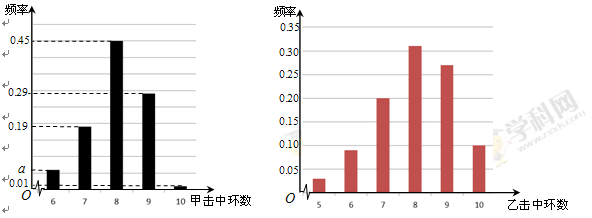
假设每名队员每次射击相互独立.
(Ⅰ)求上图中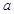 的值;
的值;
(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数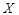 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);
(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)
(Ⅰ)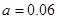 ;(Ⅱ)
;(Ⅱ)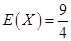 ;(Ⅲ)甲队员的射击成绩更稳定
;(Ⅲ)甲队员的射击成绩更稳定
解析试题分析:(Ⅰ)由频率和为1可求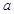 的值。(Ⅱ)从图中可以得到击中目标靶的环数不低于8环的概率,队员甲进行三次射击属于独立重复事件,符合二项分布。可根据独立重复事件概率公式
的值。(Ⅱ)从图中可以得到击中目标靶的环数不低于8环的概率,队员甲进行三次射击属于独立重复事件,符合二项分布。可根据独立重复事件概率公式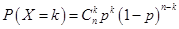 求其概率,再根据数学期望公式求其期望值,也可用二项分布列的数学期望公式求其期望值。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
求其概率,再根据数学期望公式求其期望值,也可用二项分布列的数学期望公式求其期望值。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
试题解析:解:(Ⅰ)由上图可得 ,
,
所以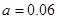 . 3分
. 3分
(Ⅱ)由图可得队员甲击中目标靶的环数不低于8环的概率为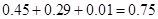 4分
4分
由题意可知随机变量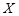 的取值为:0,1,2,3. 5分
的取值为:0,1,2,3. 5分
事件“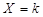 ”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环.
”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环.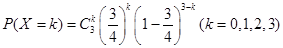
 8分
8分
即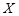 的分布列为
的分布列为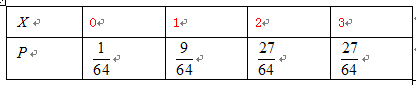
所以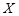 的期望是
的期望是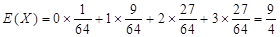 . 10分
. 10分
(Ⅲ)甲队员的射击成绩更稳定. 13分
考点:二项分布列、数学期望及方差的意义,考查数据处理能力、运算能力。


科目:高中数学 来源: 题型:解答题
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆.
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
 .记这8辆轿车的得分的平均数为
.记这8辆轿车的得分的平均数为 ,定义事件
,定义事件 {
{ ,且函数
,且函数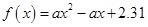 没有零点},求事件
没有零点},求事件 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市准备从7名报名者(其中男4人,女3人)中选3人到三个局任副局长.
(1)设所选3人中女副局长人数为X,求X的分布列和数学期望;
(2)若选派三个副局长依次到A、B、C三个局上任,求A局是男副局长的情况下,B局为女副局长的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
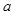 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为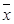 ,定义事件
,定义事件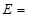 {
{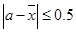 ,且函数
,且函数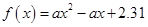 没有零点},求事件
没有零点},求事件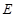 发生的概率
发生的概率 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时, =0,当四点不共面时,
=0,当四点不共面时, 的值为四点组成的四面体的体积.
的值为四点组成的四面体的体积.
(1)求概率P( =0);
=0);
(2)求 的分布列,并求其数学期望E (
的分布列,并求其数学期望E ( ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个盒子中装有形状大小相同的5张卡片,上面分别标有数字1,2,3,4,5,甲乙两人分别从盒子中随机不放回的各抽取一张.
(Ⅰ)写出所有可能的结果,并求出甲乙所抽卡片上的数字之和为偶数的概率;
(Ⅱ)以盒子中剩下的三张卡片上的数字作为边长来构造三角形,求出能构成三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
长沙市某中学在每年的11月份都会举行“社团文化节”,开幕式当天组织举行大型的文艺表演,同时邀请36名不同社团的社长进行才艺展示.其中有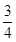 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生.
(1)若校园电视台记者随机采访3位社长,求恰有1人是高一学生且至少有1人是初中学生的概率;
(2)若校园电视台记者随机采访3位初中学生社长,设初二学生人数为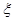 ,求
,求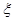 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是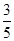 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是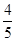 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用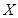 表示张同学答对题的个数,求
表示张同学答对题的个数,求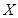 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某校高一年级学生参加社区服务次数统计,随机抽取了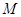 名学生作为样本,得到这
名学生作为样本,得到这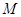 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下: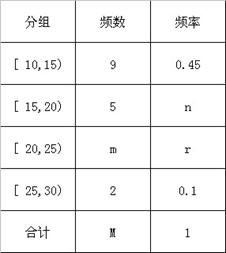
(1)求出表中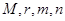 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于 次的学生中任选
次的学生中任选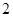 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com