
设 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时, =0,当四点不共面时,
=0,当四点不共面时, 的值为四点组成的四面体的体积.
的值为四点组成的四面体的体积.
(1)求概率P( =0);
=0);
(2)求 的分布列,并求其数学期望E (
的分布列,并求其数学期望E ( ).
).
(1)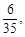
(2)
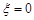
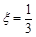
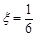
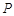

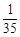
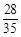
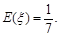
解析试题分析:(1)求概率P( = 0),就是求四点共面时概率.古典概型概率
= 0),就是求四点共面时概率.古典概型概率 的求法,关键要找出
的求法,关键要找出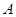 所包含的基本事件个数,然后套用公式
所包含的基本事件个数,然后套用公式
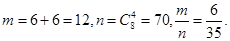 (2)求
(2)求 的数学期望的基本步骤:首先理解
的数学期望的基本步骤:首先理解 的意义,写出
的意义,写出 可能取的全部值,本题考虑四个顶点不同位置,求体积;其次求
可能取的全部值,本题考虑四个顶点不同位置,求体积;其次求 取各个值的概率,写出概率分布;最后根据概率分布,由数学期望的定义求出
取各个值的概率,写出概率分布;最后根据概率分布,由数学期望的定义求出
试题解析:(1)从正方体的八个顶点中任取四个点,共有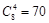 种不同取法.
种不同取法.
其中共面的情况共有12种(6个侧面,6个对角面).
则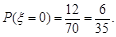 3分
3分
(2)任取四个点,当四点不共面时,四面体的体积只有以下两种情况:
①四点在相对面且异面的对角线上,体积为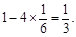
这样的取法共有2种. 5分
②四点中有三个点在一个侧面上,另一个点在相对侧面上,体积为
这样的取法共有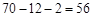 种 7分
种 7分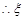 的分布列为
的分布列为
8分
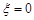
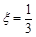
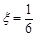
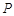

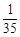
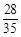
数学期望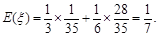 10分
10分
考点:概率,数学期望,随机变量的概率分布列.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
甲、乙两人玩一种游戏:在装有质地、大小完全相同,编号分别为1,2,3,4,5五个球的口袋中,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号和为6的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某品牌汽车4 店经销
店经销 三种排量的汽车,其中
三种排量的汽车,其中 三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买每款车型等可能.
三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买每款车型等可能.
(1)求该单位购买的3辆汽车均为 种排量汽车的概率;
种排量汽车的概率;
(2)记该单位购买的3辆汽车的排量种数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.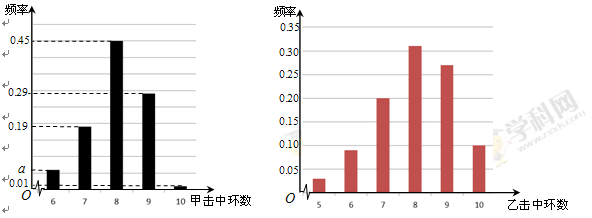
假设每名队员每次射击相互独立.
(Ⅰ)求上图中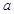 的值;
的值;
(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数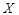 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);
(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为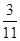 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
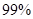 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系? 名学生从
名学生从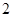 到
到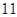 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到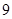 号或
号或 号的概率.
号的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为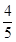 ,乙投进的概率为
,乙投进的概率为 ,求:
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com