
分析 (1)点${P_1}^/$在直线y=3x上,且在射线OP1上,利用$|O{P_1}^/|=\frac{{\sqrt{10}}}{2}$,求${P_1}^/$的坐标;
(2)利用三角形相似,证明${P_1}^/$,${P_2}^/,{P_3}^/,…{P_{2017}}^/$都在以$O{Q_1}^/$为直径的圆上,即可求出圆的方程C;
(3)求出P,R的坐标,可得直线PR的斜率.
解答 解:(1)由题意:$|O{P_1}|=2\sqrt{10}$,由$|O{P_1}||O{P_1}^/|=10$
则$|O{P_1}^/|=\frac{{\sqrt{10}}}{2}$
又点${P_1}^/$在直线y=3x上,且在射线OP1上,设点${P_1}^/(x,3x)$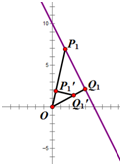
所以$\sqrt{{x^2}+9{x^2}}=\frac{{\sqrt{10}}}{2}$则${P_1}^/(\frac{1}{2},\frac{3}{2})$
证明:(2)过点O作OQ1⊥直线y=-2x+10,垂足为Q1,设Q1的“10-相好点”为${Q_1}^/$
则$|O{Q_1}||O{Q_1}^/|=10$
又∵$|O{P_1}||O{P_1}^/|=10$
∴$|O{P_1}||O{P_1}^/|=|O{Q_1}||O{Q_1}^/|$即:$\frac{{|O{P_1}|}}{{|O{Q_1}|}}=\frac{{|O{Q_1}^/|}}{{|O{P_1}^/|}}$
又$∠{P_1}O{Q_1}=∠{Q_1}^/O{P_1}^/$,
∴$△O{P_1}{Q_1}相似△O{Q_1}^/{P_1}^/$,
∴$∠O{P_1}^/{Q_1}^/=∠O{Q_1}{P_1}={90^0}$
∴${P_1}^/$在以$O{Q_1}^/$为直径的圆上,
同理可证:${P_2}^/,{P_3}^/,…{P_{2017}}^/$都在以$O{Q_1}^/$为直径的圆上
所以点${P_1}^/,{P_2}^/,…{P_{2017}}^/$共圆
由题意$\left\{\begin{array}{l}y=-2x+10\\ y=\frac{1}{2}x\end{array}\right.$联立求解,得Q1(4,2)
由于$|O{Q_1}||O{Q_1}^/|=10$且${Q_1}^/$在射线OQ1上
所以${Q_1}^/(2,1)$
则圆C的方程为:${(x-1)^2}+{(y-\frac{1}{2})^2}=\frac{5}{4}$
解:(3)由于题得M(2,0)
设直线MP的直线方程为:y=k(x-2),显然直线MR的直线方程为:y=-k(x-2)
则$\left\{\begin{array}{l}y=k(x-2)\\{(x-1)^2}+{(y-\frac{1}{2})^2}=\frac{5}{4}\end{array}\right.$可得:(k2+1)x2-(4k2+k+2)x+(4k2+2k)=0,
由韦达定理:${x_1}+{x_2}=\frac{{4{k^2}+k+2}}{{{k^2}+1}}$
因为已知一个根为2,则:${x_P}=\frac{{2{k^2}+k}}{{{k^2}+1}}$
所以点$P(\frac{{2{k^2}+k}}{{{k^2}+1}},\frac{{{k^2}-2k}}{{{k^2}+1}})$同理点$R(\frac{{2{k^2}-k}}{{{k^2}+1}},\frac{{{k^2}+2k}}{{{k^2}+1}})$
所以${k_{PR}}=\frac{{({k^2}+2k)-({k^2}-2k)}}{{(2{k^2}-k)-(2{k^2}+k)}}=-2$所以:直线PR的斜率为定值-2
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:选择题
| A. | x+3y+6=0 | B. | x-3y-6=0 | C. | 3x+y-8=0 | D. | 3x-y+8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(-∞,3)上单调递增 | |
| B. | 在(-∞,2]上单调递减,在[2,+∞)上单调递增 | |
| C. | 在[1,3]上单调递增 | |
| D. | 单调性不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,4) | B. | $(\frac{1}{2},4)$ | C. | $(-2,\frac{1}{2})$ | D. | (-3,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com