
【题目】某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果画出如图所示的频率分布直方图,其中工资收入分组区间是[10,15),[15,20),[20,25),[25,30)[30,35),[35,40](单位:百元)
(Ⅰ)为了了解工薪阶层对工资收入的满意程度,要用分层抽样的方法从调查的1000人中抽取100人做电话询问,求月工资收入在[30,35)内应抽取的人数;
(Ⅱ)根据频率分布直方图估计这1000人的平均月工资为多少元.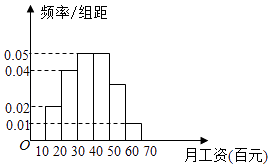
【答案】解:(Ⅰ)由频率分布直方图得月工资收入在[30,35)内的频率为:
1﹣(0.02+0.04+0.05+0.05+0.01)×5=0.15,
∴月工资收入在[30,35)内应抽取的人数为:100×0.15=15.
(Ⅱ)根据频率分布直方图估计这1000人的平均月工资为:
![]() =12.5×0.02×5+17.5×0.04×5+22.5×0.05×5+27.5×0.5×5+32.5×0.15+37.5×0.01×5=87.875(百元)=8787.5(元).
=12.5×0.02×5+17.5×0.04×5+22.5×0.05×5+27.5×0.5×5+32.5×0.15+37.5×0.01×5=87.875(百元)=8787.5(元).
【解析】(1)由频率分布直方图得月工资收入在[30,35)内的频率,由此能求出月工资收入在[30,35)内的人数,(2)根据频率分布直方图即可估计出这1000人的月平均工资.
【考点精析】掌握频率分布直方图是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: 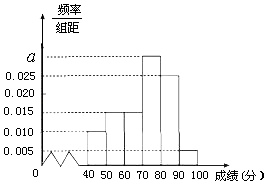
(1)求a并估计这次考试中该学科的中位数、平均值;
(2)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组…第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差不小于30分(以分数段为依据,不以具体学生分数为依据,如:[40,50),[70,80)这两组分数之差为30分),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是计算1 ![]() 的值的程序框图,则图中①、②处应填写的语句分别是( )
的值的程序框图,则图中①、②处应填写的语句分别是( )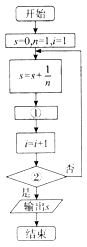
A.n=n+2,i>10?
B.n=n+2,i≥10?
C.n=n+1,i>10?
D.n=n+1,i≥10?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知cos(π+α)= ![]() ,且
,且 ![]() <α<π.
<α<π.
(Ⅰ)求5sin(α+π)﹣4tan(3π﹣α)的值
(Ⅱ)若0<β< ![]() ,cos(β﹣α)=
,cos(β﹣α)= ![]() ,求sin(
,求sin( ![]() +2β)的值.
+2β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com