
【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,P为 ![]() 上的一点,若
上的一点,若 ![]() =2,则
=2,则 ![]() 的值为 .
的值为 . 
【答案】2 ![]() ﹣2
﹣2
【解析】解:如图,连接BP,AP,设OP交AB于点M,
∵半径为2, ![]() =|
=| ![]() ||
|| ![]() |cos∠AOP=2×2×cos∠AOP=2,解得cos∠AOP=
|cos∠AOP=2×2×cos∠AOP=2,解得cos∠AOP= ![]() ,可得∠AOP=60°,
,可得∠AOP=60°,
∴由∠AOB=90°,可得:∠POB=30°,可得:∠BPO=∠PBO=75°,
又∵∠ABO=∠BAO=45°,可得:∠PBA=∠PBO﹣∠ABO=75°﹣45°=30°,
∴∠PMB=180°﹣∠OPB﹣∠PBA=180°﹣75°﹣30°=75°,
∴ ![]() =|
=| ![]() ||
|| ![]() |cos∠PMB=2×
|cos∠PMB=2× ![]() ×cos75°=4
×cos75°=4 ![]() ×cos(45°+30°)=4
×cos(45°+30°)=4 ![]() ×
× ![]() =2
=2 ![]() ﹣2.
﹣2.
所以答案是:2 ![]() ﹣2.
﹣2.

【考点精析】解答此题的关键在于理解扇形面积公式的相关知识,掌握若扇形的圆心角为![]() ,半径为
,半径为![]() ,弧长为
,弧长为![]() ,周长为
,周长为![]() ,面积为
,面积为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2cos2x,将函数y=f(x)的图象向右平移
)+2cos2x,将函数y=f(x)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
A.(﹣ ![]() ,1)
,1)
B.(﹣ ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +2x+sinx(x∈R),若函数y=f(x2+2)+f(﹣2x﹣m)只有一个零点,则函数g(x)=mx+
+2x+sinx(x∈R),若函数y=f(x2+2)+f(﹣2x﹣m)只有一个零点,则函数g(x)=mx+ ![]() (x>1)的最小值是 .
(x>1)的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线 ![]() 是函数f(x)=sinx+acosx的图象的一条对称轴.
是函数f(x)=sinx+acosx的图象的一条对称轴.
(1)求函数f(x)的最大值及取得最大值时x的值;
(2)求函数f(x)在[0,π]上的减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O,半径为R,矩形的一边AB在直径上,点C,D,G,H在圆周上,E,F在边CD上,且 ![]() ,设∠BOC=θ.
,设∠BOC=θ.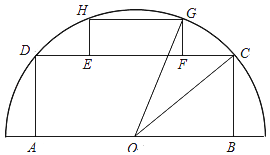
(1)记游泳池及其附属设施的占地面积为f(θ),求f(θ)的表达式;
(2)怎样设计才能符合园林局的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是圆O上的三个点,CO的延长线与线段BA的延长线交于圆外一点.若 ![]() ,其中m,n∈R.则m+n的取值范围是( )
,其中m,n∈R.则m+n的取值范围是( )
A.(0,1)
B.(﹣1,0)
C.(1,+∞)
D.(﹣∞,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=BC,点M为棱A1B1的中点.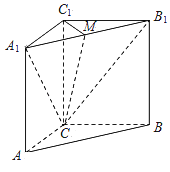
求证:
(1)AB∥平面A1B1C;
(2)平面C1CM⊥平面A1B1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,且椭圆E上的点到点F的距离的最小值为2.
,右焦点为F,且椭圆E上的点到点F的距离的最小值为2.
(1)求a,b的值;
(2)设椭圆E的左、右顶点分别为A,B,过点A的直线l与椭圆E及直线x=8分别相交于点M,N
①当过点A,F,N三点的圆半径最小时,求这个圆的方程;②若cos∠AMB= ![]() ,求△ABM的面积.
,求△ABM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com