
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=BC,点M为棱A1B1的中点.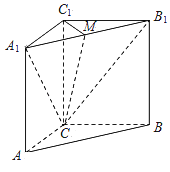
求证:
(1)AB∥平面A1B1C;
(2)平面C1CM⊥平面A1B1C.
【答案】
(1)证明:∵AA1∥BB1,AA1=BB1,
∴四边形AA1B1B是平行四边形,
∴AB∥A1B1,
又AB平面A1B1C,A1B1平面A1B1C,
∴AB∥平面A1B1C
(2)证明:由(1)证明同理可知AC=A1C1,BC=B1C1,
∵AC=BC,∴A1C1=B1C1,
∵M是A1B1的中点,
∴C1M⊥A1B1,
∵CC1⊥平面A1B1C1,B1A1平面A1B1C1,
∴CC1⊥B1A1,
又CC1∩C1M=C1,
∴B1A1⊥平面C1CM,
又B1A1平面A1B1C1,
∴平面C1CM⊥平面A1B1C
【解析】(1)只要证出AB![]() A1B1即可;(2)只要证出A1B1
A1B1即可;(2)只要证出A1B1![]() C1M、A1B1
C1M、A1B1![]() CC1即可.
CC1即可.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足f(x+3)=2f(x),当x∈[﹣1,2)时,f(x)= 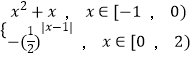 .
.
若存在x∈[﹣4,﹣1),使得不等式t2﹣3t≥4f(x)成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中, ![]() =(2,﹣2),
=(2,﹣2), ![]() =(x,y),
=(x,y), ![]() =(1,
=(1, ![]() ).
).
(1)若 ![]() ∥
∥ ![]() ,求x,y之间的关系式;
,求x,y之间的关系式;
(2)满足(1)的同时又有 ![]() ⊥
⊥ ![]() ,求x,y的值以及四边形ABCD的面积.
,求x,y的值以及四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OA是南北方向的一条公路,OB是北偏东45°方向的一条公路,某风景区的一段边界为曲线C.为方便游客光,拟过曲线C上的某点分别修建与公路OA,OB垂直的两条道路PM,PN,且PM,PN的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy,则曲线符合函数y=x+ ![]() (1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.
(1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.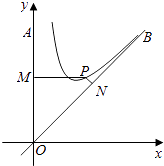
(1)求f(x)解析式;
(2)当x为多少时,总造价f(x)最低?并求出最低造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:对任意的 ![]() ,sinx≤ax+b≤tanx恒成立,其中a,b∈R.
,sinx≤ax+b≤tanx恒成立,其中a,b∈R.
(1)若a=1,b=0,求证:命题p为真命题.
(2)若命题p为真命题,求a,b的所有值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(﹣1,0),B(1,1),C(2,0),点P是平面直角坐标系xOy上一点,且 ![]() =m
=m ![]() (m,n∈R),
(m,n∈R),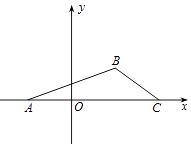
(1)若m=1,且 ![]() ∥
∥ ![]() ,试求实数n的值;
,试求实数n的值;
(2)若点P在△ABC三边围成的区域(含边界)上,求m+3n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(I)如果 ![]() 在
在 ![]() 处取得极值,求
处取得极值,求 ![]() 的值.
的值.
(II)求函数 ![]() 的单调区间.
的单调区间.
(III)当 ![]() 时,过点
时,过点 ![]() 存在函数曲线
存在函数曲线 ![]() 的切线,求
的切线,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(1+x)+alog2(1﹣x)(a∈R)的图象关于y轴对称.
(1)求函数f(x)的定义域;
(2)求a的值;
(3)若函数g(x)=x﹣2f(x)﹣2t有两个不同的零点,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com