
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.

(1)求证:![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)在(2)的条件下,侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() .若存在,求
.若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
【答案】(1)见证明;(2) ![]() (3)见解析
(3)见解析
【解析】
(1)先证明![]() 平面
平面![]() ,即可得到
,即可得到![]() ;
;
(2)由题设知,连![]() ,设
,设![]() 交于
交于![]() 于
于![]() ,由题意知
,由题意知![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立空间直角坐标系,分别求出平面
轴正方向,建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,求法向量的夹角余弦值,即可求出结果;
的一个法向量,求法向量的夹角余弦值,即可求出结果;
(3)要使![]() 平面
平面![]() ,只需
,只需![]() 与平面的法向量垂直即可,结合(2)中求出的平面
与平面的法向量垂直即可,结合(2)中求出的平面![]() 的一个法向量,即可求解.
的一个法向量,即可求解.
(1)连![]() 交
交![]() 于
于![]() ,由题意
,由题意![]() .
.
在正方形![]() 中,
中,![]() ,
,
所以![]() 平面
平面![]() ,得
,得![]()
(2)由题设知,连![]() ,设
,设![]() 交于
交于![]() 于
于![]() ,由题意知
,由题意知![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立坐标系
轴正方向,建立坐标系![]() 如图.
如图.
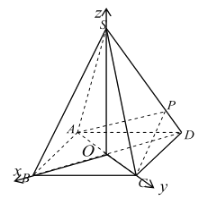
设底面边长为![]() ,则高
,则高![]() .
.
则![]() ,
,![]() ,
,![]()
又![]() 平面
平面![]() ,
,
则平面![]() 的一个法向量
的一个法向量![]() ,
,
平面![]() 的一个法向量
的一个法向量![]() ,
,
则![]() ,
,
又二面角![]() 为锐角,则二面角
为锐角,则二面角![]() 为
为![]() ;
;
(3)在棱![]() 上存在一点
上存在一点![]() 使
使![]() 平面
平面![]() .由(2)知
.由(2)知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
且![]() ,
,![]()
设![]() ,
,![]()
则![]()
![]()
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
则![]() .
.
即当![]() 时,
时,![]()
而![]() 不在平面
不在平面![]() 内,故
内,故![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),以直角坐标系原点为极点,x轴非负半轴为极轴并取相同的单位长度建立极坐标系,
为参数),以直角坐标系原点为极点,x轴非负半轴为极轴并取相同的单位长度建立极坐标系,
(1)求曲线C的极坐标方程,并说明其表示什么轨迹;
(2)若直线l的极坐标方程为![]() ,求曲线C上的点到直线l的最大距离.
,求曲线C上的点到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: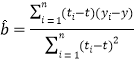 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5名运动员参加一次乒乓球比赛,每![]() 名运动员都赛
名运动员都赛![]() 场并决出胜负.设第
场并决出胜负.设第![]() 位运动员共胜
位运动员共胜![]() 场,负
场,负![]() 场(
场(![]() ),则错误的结论是( )
),则错误的结论是( )
A. ![]()
B. ![]()
C. ![]() 为定值,与各场比赛的结果无关
为定值,与各场比赛的结果无关
D. ![]() 为定值,与各场比赛结果无关
为定值,与各场比赛结果无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]()
![]() .对于
.对于![]() ,定义
,定义![]() 与
与![]() 之间的距离为
之间的距离为![]() .
.
(Ⅰ)![]() ,写出所有
,写出所有![]() 的
的![]() ;
;
(Ⅱ)任取固定的元素![]() ,计算集合
,计算集合![]() 中元素个数;
中元素个数;
(Ⅲ)设![]() ,
,![]() 中有
中有![]() 个元素,记
个元素,记![]() 中所有不同元素间的距离的最小值为
中所有不同元素间的距离的最小值为![]() .证明:
.证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①若线性回归方程为![]() ,则当变量
,则当变量![]() 增加一个单位时,
增加一个单位时,![]() 一定增加3个单位;②将一组数据中的每个数据都加上同一个常数后,方差不会改变;③线性回归直线方程
一定增加3个单位;②将一组数据中的每个数据都加上同一个常数后,方差不会改变;③线性回归直线方程![]() 必过点
必过点![]() ;④抽签法属于简单随机抽样;其中错误的说法是( )
;④抽签法属于简单随机抽样;其中错误的说法是( )
A.①③B.②③④C.①D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
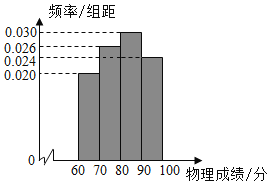
【题目】为了解某校高一1000名学生的物理成绩,随机抽查了部分学生的期中考试成绩,将数据整理后绘制成如图所示的频率分布直方图.
(1)估计该校高一学生物理成绩不低于80分的人数;
(2)若在本次考试中,规定物理成绩在m分以上(包括m分)的为优秀,该校学生物理成绩的优秀率大约为18%,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的正半轴重合,且长度单位相同;曲线
轴的正半轴重合,且长度单位相同;曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),设
),设![]() , 直线
, 直线![]() 与曲线
与曲线![]() 交于
交于 ![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长度;
的长度;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com