
分析 作出函数的图象,利用图象结合已知条件,利用消元法将n•g(m)转化为关于n的一元二次函数进行求解即可得到结论.
解答 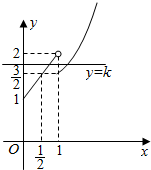 解:作出函数h(x)=$\left\{\begin{array}{l}{f(x),0≤x<1}\\{g(x),x≥1}\end{array}\right.$,的图象,
解:作出函数h(x)=$\left\{\begin{array}{l}{f(x),0≤x<1}\\{g(x),x≥1}\end{array}\right.$,的图象,
若方程h(x)-k=0,k∈[$\frac{3}{2}$,2)有两个不同的实根m,n(m>n≥0),则:$\frac{1}{2}≤n<1$,
ng(m)=nf(n)=n(n+1)=n2+n=(n+$\frac{1}{2}$)2-$\frac{1}{4}$,
∴$\frac{3}{4}$≤n•g(m)<2,
故答案为:[$\frac{3}{4}$,2)
点评 本题考查函数与方程的综合应用,一次函数二次函数指数函数的值域等知识,作出函数的图象是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
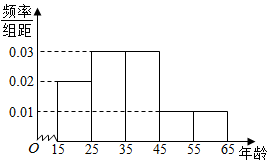 中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65的人群中随机调查50人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如表:
中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65的人群中随机调查50人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如表:| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 支持“延迟退休”人数 | 5 | 10 | 10 | 2 | 1 |
| 45岁以下 | 45岁以上 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (0,1) | C. | (-2,2) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆与直线相切 | B. | 圆与直线相交 | ||
| C. | 圆与直线相离 | D. | 以上三种均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$,2 | B. | $\frac{1}{4}$,4 | C. | $\frac{1}{4}$,2 | D. | $\frac{1}{2}$,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com