
已知椭圆 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 右焦点
右焦点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 (点
(点 在第一象限).
在第一象限).
(1)求椭圆 的方程;
的方程;
(2)已知 为椭圆
为椭圆 的左顶点,平行于
的左顶点,平行于 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.
(1)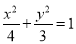 ;(2)对称.
;(2)对称.
【解析】
试题分析:(1)由圆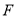 方程可知圆心为
方程可知圆心为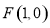 ,即
,即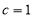 ,又因为离心率为
,又因为离心率为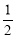 ,可得
,可得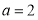 ,根据椭圆中关系式
,根据椭圆中关系式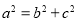 ,可求
,可求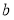 ,椭圆方程即可写出;(2)由椭圆方程可知
,椭圆方程即可写出;(2)由椭圆方程可知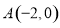 ,将
,将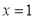 代入椭圆方程可得
代入椭圆方程可得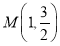 ,可得
,可得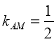 ,设直线
,设直线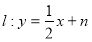 ,设
,设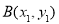 ,
,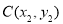 ,然后和椭圆方程联立,消掉
,然后和椭圆方程联立,消掉 (或
(或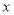 )得到关于
)得到关于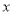 的一元二次方程,再根据韦达定理得出根与系数的关系,可得两直线
的一元二次方程,再根据韦达定理得出根与系数的关系,可得两直线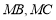 的斜率.若直线
的斜率.若直线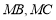 是关于直线
是关于直线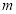 对称时两直线倾斜角互补,所以斜率互为相反数,把求得的两直线斜率相加若为0,则说明两直线对称,否则不对称.
对称时两直线倾斜角互补,所以斜率互为相反数,把求得的两直线斜率相加若为0,则说明两直线对称,否则不对称.
试题解析:(1)由题意得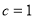 , 由
, 由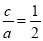 可得
可得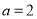 , 所以
, 所以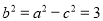
所以椭圆的方程为 . 4分
. 4分
(2)由题意可得点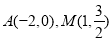
所以由题意可设直线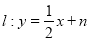 ,
,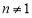
设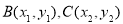
由 得
得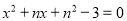
由题意可得 ,即
,即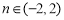 且
且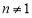
 6分
6分
因为 8分
8分
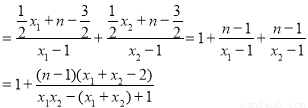
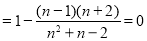 , 10分
, 10分
所以直线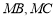 关于直线
关于直线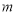 对称 12分.
对称 12分.
考点:1.椭圆的基础知识;2.直线与椭圆的位置关系;3.二次方程根与系数的关系.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源:2015届河北省高二下学期第一次月考文科数学试卷(解析版) 题型:选择题
一名小学生的年龄和身高(单位:cm)的数据如下:
年龄 | 6 | 7 | 8 | 9 |
身高 | 118 | 126 | 136 | 144 |
由散点图可知,身高 与年龄
与年龄 之间的线性回归直线方程为
之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A.154 B. 153 C.152 D. 151
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试理科数学试卷(解析版) 题型:填空题
已知双曲线C: (a>0,b>0)的一条渐近线与直线l:
(a>0,b>0)的一条渐近线与直线l: 垂直,C的一个焦点到l的距离为1,则C的方程为__________________.
垂直,C的一个焦点到l的距离为1,则C的方程为__________________.
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为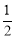 与
与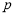 ,且乙投球
,且乙投球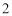 次均未命中的概率为
次均未命中的概率为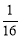 .
.
(1)求乙投球的命中率 ;
;
(2)若甲投球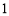 次,乙投球
次,乙投球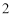 次,两人共命中的次数记为
次,两人共命中的次数记为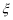 ,求
,求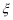 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com