
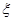 ,求
,求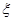 的分布列和数学期望.
的分布列和数学期望. 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 76 | 81 |
 的分布列及其期望.
的分布列及其期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立. ,求随机变量
,求随机变量 的
的查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com