
| 1 |
| 2 |
| 7 |
| 36 |
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 分别表示英语成绩和数学成绩的等级分(例如表中英语成绩等级分为5分的共6人,数学成绩等级分为3分的共15人).由已知表格,试填写出对应的表格(见答题卷中的表格).也即求出下列各对应值:
分别表示英语成绩和数学成绩的等级分(例如表中英语成绩等级分为5分的共6人,数学成绩等级分为3分的共15人).由已知表格,试填写出对应的表格(见答题卷中的表格).也即求出下列各对应值: 的概率P
的概率PA.;(2) 且 且 的概率P 的概率P | B.; (3)  的概率P 的概率P | C.;(4) 且 且 的概率P 的概率P | D.; |
 的概率P(E)及对应的
的概率P(E)及对应的 的值.
的值.  | 5 | 4 | 3 | 2 | 1 |
| 5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 7 | 5 | 1 |
| 3 | 2 | 1 | 0 | 9 | 3 |
| 2 | 1 |  | 6 | 0 | 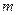 |
| 1 | 0 | 0 | 1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.A与B | B.B与C | C.C与D | D.A与D |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 2 |
| 3 |
| 2 |
| 5 |
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.对立事件 | B.互斥但不对立事件 |
| C.不可能事件 | D.以上都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.“甲站排头”与“乙站排头” |
| B.“甲站排头”与“乙站排尾” |
| C.“甲站排头”与“乙不站排头” |
| D.“甲不站排头”与“乙不站排头” |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com