
���� ��1��ֱ�߹����㣨3��0����֪����F��3��0�����ɵ������ʣ�
��2����ֱ�߲�����������Բ�������������ò����ļ���������|MF|•|NF|�����ֵ��
��� �⣺��1��ֱ�߹����㣨3��0����֪����F��3��0������������Ϊ$\frac{3}{5}$��5�֣�
��2����ֱ�߲�����������Բ���������ã�16��tcos��+3��2+25��tsin����2=25��16��
����ã�16cos2��+25sin2����t2+96tcos��-32��8=0��
��$|{{t_1}{t_2}}|=\frac{32��8}{{16{{cos}^2}��+25{{sin}^2}��}}=\frac{32��8}{{16+9{{sin}^2}��}}��16$��
��|MF|•|NF|�����ֵΪ16 ��10�֣�
���� ���⿼��ֱ�ߡ���Բ�IJ������̣�����ֱ������Բ��λ�ù�ϵ���������������������ã������е��⣮


 �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 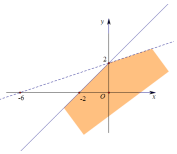 | B�� | 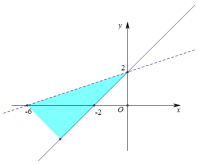 | ||
| C�� | 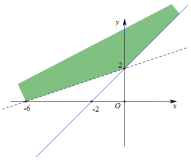 | D�� | 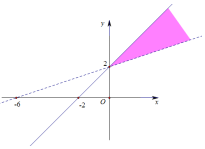 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
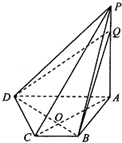 ��ͼ��������P-ABCD�У�PA�͵���ABCD������ABCDΪֱ�����Σ���ABC=��DAB=$\frac{��}{2}$��AC��BD���ڵ�O��BD��PC��AB=2$\sqrt{3}$����BC=2��PA=6��
��ͼ��������P-ABCD�У�PA�͵���ABCD������ABCDΪֱ�����Σ���ABC=��DAB=$\frac{��}{2}$��AC��BD���ڵ�O��BD��PC��AB=2$\sqrt{3}$����BC=2��PA=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | Ů | �ܼ� | |
| ϲ������ʳ | 5 | 12 | 17 |
| ��ϲ������ʳ | 40 | 28 | 68 |
| �ܼ� | 45 | 40 | 85 |
| P��K2��k�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com