
分析 首先考虑函数的定义域优先原则求出定义域,然后对函数求导,导函数小于等于零,函数是单调减函数,求出减区间,即可得到单调增区间,也可获得极值.
解答 解:由题意可知函数的定义域为:(0,+∞)
又f′(x)=4x•lnx+2•x2•$\frac{1}{x}$=4x•lnx+2x,
由f′(x)≤0知,2x•lnx+x≤0,
∴0≤x≤${e}^{-\frac{1}{2}}$,
又因为x>0,所以函数的递减区间是(0,${e}^{-\frac{1}{2}}$].函数的单调增区间为(${e}^{-\frac{1}{2}}$,+∞),
函数在x=${e}^{-\frac{1}{2}}$时函数取得极小值:y极小=f(${e}^{-\frac{1}{2}}$)=-$\frac{1}{e}$.
点评 此题考查的是函数的单调性和导数知识的综合问题.在解答过程当中充分体现了定义于优先的原则、求导的思想、问题转化的思想.值得同学们体会反思.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
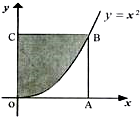
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com