
分析 (Ⅰ)直接根据三角函数周期公式进行求解即可,根据正弦函数的减区间建立关系式,可求出函数f(x)的单调递减区间.
(Ⅱ)由$0≤x≤\frac{π}{2}$ 得$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{5π}{6}$,即可求f(x)的值域.
解答 解:(Ⅰ)函数f(x) 的最小正周期为π,…2分
又由$2kπ+\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{3π}{2},k∈z$ 得$kπ+\frac{π}{3}≤x≤2kπ+\frac{5π}{3},k∈z$,
所以函数的单调递减区间为:[k$π+\frac{π}{3}$,2kπ+$\frac{5π}{3}$](k∈Z)…5分
(Ⅱ)由$0≤x≤\frac{π}{2}$ 得$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{5π}{6}$,…7分
所以$-\frac{1}{2}≤sin({2x-\frac{π}{6}})≤1$ …10分
所以$-2≤2sin({2x-\frac{π}{6}})-1≤1$ …11分
所以值域:[-2,1]…12分
点评 本题考查了形如y=Asin(ωx+φ)的形式的周期性,以及最值的求解和函数的单调性.一般情况下,要研究形如y=Asin(ωx+φ)的形式的函数,都会将ωx+φ看作一个整体,利用正弦函数和余弦函数的图象和性质求解.属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 喜欢吃零食 | 5 | 12 | 17 |
| 不喜欢吃零食 | 40 | 28 | 68 |
| 总计 | 45 | 40 | 85 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
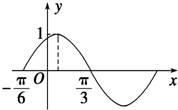 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{\sqrt{3}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com