
分析 (1)先求出切线方程,再构造g(x)=(2-x) ex-x-2,证明g(x)递减,又g(0)=0,所以g(x)≤0,即可得出结论;
(2)由(1)知:(2-x) ex≤x-2,则$f(\frac{1}{n}-\frac{1}{n+1})<2+\frac{1}{n}-\frac{1}{n+1}$,设h(x)=ex-x-1,h'(x)=ex-1,证明 ex>x+1在x≥0时恒成立,即可证明结论.
解答 证明:(1)f'(x)=(1-x) ex,f(0)=2,f'(0)=1,所以l:y=x+2…(1分)
设g(x)=(2-x) ex-x-2,g'(x)=f(x)-(x+2)=(1-x) ex-1,…(2分)
g''(x)=-x ex,当x≥0时,g''(x)<0,g'(x)递减,
又g'(0)=0,∴g'(x)≤0,…(4分)
所以g(x)递减,
又g(0)=0,所以g(x)≤0,
所以f(x)≤x+2,即f(x)图象在l下方…(5分)
(2)由(1)知:(2-x) ex≤x-2,则$f(\frac{1}{n}-\frac{1}{n+1})<2+\frac{1}{n}-\frac{1}{n+1}$…(6分)
设h(x)=ex-x-1,h'(x)=ex-1,
当x≥0时,h'(x)>0,所以h(x)=ex-x-1在x≥0时递增,而h(0)=0,
所以h(x)>0,即ex>x+1在x≥0时恒成立,
所以${e^{\frac{1}{n}}}>\frac{1}{n}+1$,所以$\frac{1}{{{e^{\frac{1}{n}}}}}<\frac{1}{{\frac{1}{n}+1}}$,即${e^{-\frac{1}{n}}}<\frac{n}{n+1}$.…(10分)
于是$\frac{1}{e^2}f(2-\frac{1}{n})=\frac{1}{e^2}[2-(2-\frac{1}{n})]{e^{2-\frac{1}{n}}}=\frac{1}{n}{e^{-\frac{1}{n}}}<\frac{1}{n+1}$,…(11分)
所以$f(\frac{1}{n}-\frac{1}{n+1})+\frac{1}{e^2}f(2-\frac{1}{n+1})<2+\frac{1}{n}-\frac{1}{n+1}+\frac{1}{n+1}=2+\frac{1}{n}$…(12分)
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
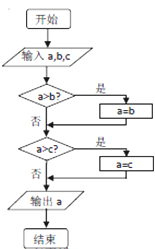
| A. | 20.1 | B. | ln$\frac{1}{3}$ | C. | π-1 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
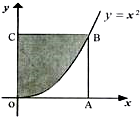
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com