练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．观察下列数表：

    设1025是该表第m行的第n个数，则m+n=12．

    分析 根据上面数表的数的排列规律，1、3、5、7、9…都是连续奇数，第一行1个数，第二行2个数，第三行4个数，第四行8个数，…第10行有29个数，分别求出左起第1个数的规律，按照此规律，求出答案即可．

    解答 解：根据上面数表的数的排列规律，1、3、5、7、9…都是连续奇数，
    第一行1个数，
    第二行2=21个数，且第1个数是3=22-1
    第三行4=22个数，且第1个数是7=23-1
    第四行8=23个数，且第1个数是15=24-1
        …
    第10行有29个数，且第1个数是210-1=1023，
    第2个数为1025，第三个数为1027；所以1027是第10行的第3个数，所以m=10，n=2，
    所以m+n=12；
    故答案为：12．

    点评 本题主要考查归纳推理的问题，关键是根据数表，认真分析，找到规律，然后进行计算，即可解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=x3-6x+5，x∈R．
    （1）求函数f（x）在x=1处的切线方程；
    （2）求f（x）在区间[-2，2]的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．求函数y=2lnx•x2的单调区间和极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．将函数f（x）=2sin（ωx+$\frac{π}{3}}$）（ω＞0）的图象向右平移$\frac{π}{3ω}$个单位，得到函数y=g（x）的图象，若y=g（x）在$[{-\frac{π}{3}，\frac{π}{4}}]$上为增函数，则ω的最大值为（　　）
    A．1B．2C．$\frac{3}{2}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

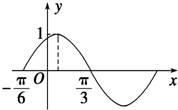    11．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若x1，x2∈（-$\frac{π}{6}$，$\frac{π}{3}$），且f（x1）=f（x2），则f（x1+x2）=$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设i为虚数单位，复数z=$\frac{2i}{1+i}$$，\overline z$为复数z的共轭复数，则$|{\overline z}$|=（　　）
    A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=（2-x） ex，曲线f（x）在x=0处的切线方程为l．
    （1）求证：当x≥0时，f（x）图象在l下方；
    （2）若n∈N*，求证：f（$\frac{1}{n}$-$\frac{1}{n+1}$）+$\frac{1}{e^2}$f（2-$\frac{1}{n}$）≤2+$\frac{1}{n}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设函数f（x）=x2+ax+b（a，b∈R）．已知当|x|≤1时，|f（x）|≤1恒成立．
    （1）若a=0，求实数b的取值范围；
    （2）求a-3b的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知关于的不等式$\frac{ax-3}{{x}^{2}-a}$≤0的解集为M．
    （1）若3∈M，且5∉M，求实数a的取值范围；
    （2）若a＞3，求集合M．

    查看答案和解析>>

    同步练习册答案